题目内容
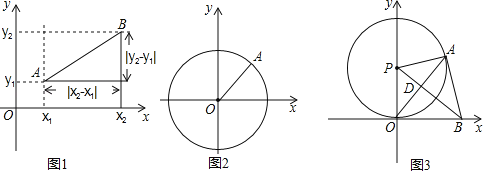
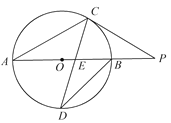
【题目】已知：AB为⊙O的直径，延长AB到点P，过点P作圆O的切线，切点为C，连接AC，且AC=CP.
（1）求∠P的度数；
（2）若点D是弧AB的中点，连接CD交AB于点E，且DE·DC=20，求⊙O的面积.（π取3.14）
【答案】（1）∠P=30°；（2）31.4.
【解析】
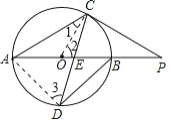
（1）连接OC，根据圆的切线的性质可得∠2＋∠P＝90°，根据等腰三角形的性质可得∠P＝∠CAO，再根据三角形外角的性质可得∠2＝2∠P，进而可求出∠P的度数；（2）连接AD，根据等弧对等角得到∠ACD＝∠DAE，故△ACD∽△DAE，然后根据相似比求出AD的长，再根据“直径所对的角是90°”以及AD＝BD得到Rt△ADB是等腰直角三角形，根据等腰直角三角形的性质求出OA的长，进而可求出⊙O的面积.
（1）连接
，
为
的切线，
，即
，
，
，
，
，
又
是
的一个外角，
，
，
；
（2）连接
，
为
的中点，
，
，
，即
，
，
，
，
，
是的直径，
为等腰直角三角形，
，
，
．
练习册系列答案
相关题目
