题目内容
【题目】已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连结OA、OP.当OA⊥OP时,P点坐标为 . 
【答案】(2,﹣4)
【解析】解:∵抛物线y=ax2+x的对称轴为直线x=2, ∴﹣ ![]() =2,
=2,
∴a=﹣ ![]() ,
,
∴抛物线的表达式为:y=﹣ ![]() x2+x,
x2+x,
∴顶点A的坐标为(2,1),
设对称轴与x轴的交点为E.
如图,在直角三角形AOE和直角三角形POE中,tan∠OAE= ![]() ,tan∠EOP=
,tan∠EOP= ![]() ,
,
∵OA⊥OP,
∴∠OAE=∠EOP,
∴ ![]() =
= ![]() ,
,
∵AE=1,OE=2,
∴ ![]() =
= ![]() ,
,
解得PE=4,
∴P(2,﹣4),
所以答案是:(2,﹣4).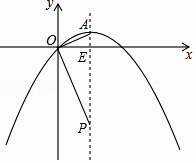
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
相关题目