题目内容
【题目】 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E. 
(1)求证:AC平分∠DAB;
(2)若∠B=60°,CD=2 ![]() ,求AE的长.
,求AE的长.
【答案】
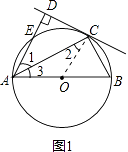
(1)证明:如图1,连接OC,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∵AD⊥CD,
∴∠ADC=90°,
∴∠OCD+∠ADC=180°,
∴AD∥OC,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
则AC平分∠DAB
(2)解:
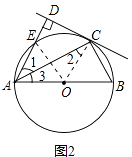
法1:如图2,连接OE,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠B=60°,
∴∠1=∠3=30°,
在Rt△ACD中,CD=2 ![]() ,∠1=30°,
,∠1=30°,
∴AC=2CD=4 ![]() ,
,
在Rt△ABC中,AC=4 ![]() ,∠CAB=30°,
,∠CAB=30°,
∴AB= ![]() =
= ![]() =8,
=8,
∵∠EAO=2∠3=60°,OA=OE,
∴△AOE是等边三角形,
∴AE=OA= ![]() AB=4;
AB=4;
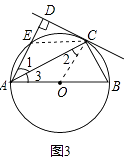
法2:如图3,连接CE,
∵AB为⊙O的直径,
∴∠ACB=90°,
又∠B=60°,
∴∠1=∠3=30°,
在Rt△ACD中,CD=2 ![]() ,
,
∴AD= ![]() =
= ![]() =6,
=6,
∵四边形ABCE是⊙O的内接四边形,
∴∠B+∠AEC=180°,
又∵∠DEC=∠B=60°,
在Rt△CDE中,CD=2 ![]() ,
,
∴DE= ![]() =
= ![]() =2,
=2,
∴AE=AD﹣DE=4.
【解析】(1)连接OC,由CD为圆O的切线,根据切线的性质得到OC垂直于CD,由AD垂直于CD,可得出OC平行于AD,根据两直线平行内错角相等可得出∠1=∠2,再由OA=OC,利用等边对等角得到∠2=∠3,等量代换可得出∠1=∠3,即AC为角平分线;(2)法1:由AB为圆O的直径,根据直径所对的圆周角为直角可得出∠ACB为直角,在直角三角形ABC中,由∠B的度数求出∠3的度数为30°,可得出∠1的度数为30°,在直角三角形ACD中,根据30°角所对的直角边等于斜边的一半,由CD的长求出AC的长,在直角三角形ABC中,根据cos30°及AC的长,利用锐角三角函数定义求出AB的长,进而得出半径OE的长,由∠EAO为60°,及OE=OA,得到三角形AEO为等边三角形,可得出AE=OA=OE,即可确定出AE的长;法2:连接EC,由AB为圆O的直径,根据直径所对的圆周角为直角可得出∠ACB为直角,在直角三角形ABC中,由∠B的度数求出∠3的度数为30°,可得出∠1的度数为30°,在直角三角形ADC中,由CD及tan30°,利用锐角三角函数定义求出AD的长,由∠DEC为圆内接四边形ABCE的外角,利用圆内接四边形的外角等于它的内对角,得到∠DEC=∠B,由∠B的度数求出∠DEC的度数为60°,在直角三角形DEC中,由tan60°及DC的长,求出DE的长,最后由AD﹣ED即可求出AE的长.
【考点精析】通过灵活运用圆周角定理和切线的性质定理,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题.

【题目】将自然数按如表规律排列,表中数2在第二行第一列,与有序数对![]() 对应,数5与
对应,数5与![]() 对应,数14与
对应,数14与![]() 对应,根据这一规律,数2014对应的有序数对为__________.
对应,根据这一规律,数2014对应的有序数对为__________.
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | ||
第一行 | 1 | 4 | 5 | 16 | 17 | … |
第二行 | 2 | 3 | 6 | 15 | … | |
第三行 | 9 | 8 | 7 | 14 | … | |
第四行 | 10 | 11 | 12 | 13 | … | |
第五行 | … | |||||
…… |