Question

【题目】如图，四边形ABCD中，AB=AD，BC=DC，∠A=90°，∠ABC=105°．若AB=5 ，则△ABD外心与△BCD外心的距离为何？（　　）
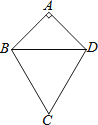
A.5
B.5
C.
D.

Answer 1

【答案】A
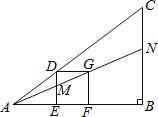
【解析】解：如图，连接AC，作DF⊥BC于F，AC与BD、DF交于点E、G．
∵AB=AD，CB=CD，
∴AC垂直平分BD，
∵∠BAD=90°，
∴∠ABD=∠ADB=45°，
∵∠ABC=105°，
∴∠CBD=60°，∵CB=CD，
∴△BCD是等边三角形，△ABD是等腰直角三角形，
∴点E是△BAD的外心，点G是△BCD的外心，
在RT△ABD中，∵AB=AD=5 ，∴BD=10 ，∴BE=DE=5 ，在RT△EDG中，∵∠DEG=90°，∠EDG=30°，ED=5 ，∴tan30°= ，
∴EG=5．
∴△ABD外心与△BCD外心的距离为5．
故选A．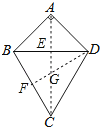

【考点精析】本题主要考查了三角形的外接圆与外心的相关知识点，需要掌握过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心才能正确解答此题．