题目内容
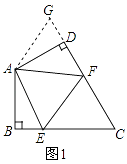
【题目】如图的△ABC中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点．若∠B=90°，AB=4，BC=3，EF=1，则BN的长度为何？（ ）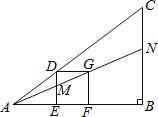 
A.
B.
C.
D.
【答案】D
【解析】解：∵四边形DEFG是正方形，
∴DE∥BC，GF∥BN，且DE=GF=EF=1，
∴△ADE∽△ACB，△AGF∽△ANB，
∴ 
①， 
②，由①可得， 
，解得：AE= 
，将AE= 
代入②，得：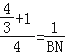 
，解得：BN= 
，
故选：D．
由DE∥BC可得 求出AE的长，由GF∥BN可得 ，将AE的长代入可求得BN．本题主要考查正方形的性质及相似三角形的判定与性质，根据相似三角形的性质得出AE的长是解题的关键．
练习册系列答案
相关题目
