题目内容
【题目】如图1，点P为△ABC边上一动点，沿着A→C→B的路径行进，点P作PD⊥AB，垂足为D，设AD＝x，△APD的面积为y，图2是y关于x的函数图象，则依据图中的数量关系计算△ACB的周长为（ ）
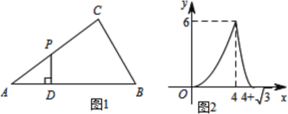
A.
B.15C.
D.
【答案】C
【解析】
根据函数图象得出拐点处坐标为（4，6），结合图3得出当点P运动到C点时，y有最大值6，从而计算出CD的值，勾股定理求出AC，根据当点D运动到B点时，函数值为0，求出AB的值，从而求出BD的值，利用锐角三角函数求出BC即可解答．
由图像可知函数图像的拐点处坐标为（4，6），
结合图3可知，当点P运动到C点时，y有最大值6，
可知：y=
AD·CD，代入数据得CD=3，
在Rt△ADC中，AC=
=5，
当点D运动到B点时，函数值为0，故AB=
，
∴BD=4+
-4=，
在Rt△BDC中，CD=3，BD=，tanB=，
得∠B=60°，由BD=BC·cos60°，得BC=
，
∴△ABC的周长为：5++4 += 
．
故选：C．
优生乐园系列答案【题目】某校为了了解学生的身高情况，随机对该校男生、女生的身高进行抽样调查，已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制成下面的统计图表：
组别 | A | B | C | D | E |
身高（cm） | x＜150 | 150≤x＜155 | 155≤x＜160 | 160≤x＜165 | x≥165 |
根据图表中信息，回答下列问题：
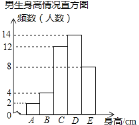
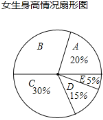
（1）在样本中，男生身高的中位数落在 组（填组别序号），女生身高在B组的人数有 人；
（2）已知该校共有男生500人，女生480人，请估计身高在155≤x＜165之间的学生约有多少人？
（3）从男生样本的A、B两组里，随机安排2人参加一项活动，求恰好是1人在A组、1人在B组的概率．
【题目】复课返校后，为了让同学们进一步了解“新型冠状病毒”的防控知识，某学校组织了一次关于“新型冠状病毒”的防控知识比赛，从问卷中随机抽查了一部分，对调查结果进行了分组统计，并制作了如下表格与条形统计图：
分组结果 | 频数 | 频率 |
A.完全掌握 | 30 | 0.3 |
B.比较清楚 | 50 |
|
C.不怎么清楚 |
| 0.15 |
D.不清楚 | 5 | 0.05 |
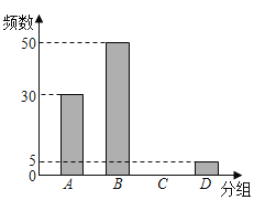
请根据上图完成下面题目：
（1）总人数为 人，
，
；
（2）请你补全条形统计图；
（3）若全校有2700人，请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少．
【题目】对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏温度之间是一次函数关系．如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位
)，右边为华氏温度的刻度和读数(单位
)．从温度计的刻度上可以看出，摄氏温度
与华氏温度
部分对应关系如下表：
| ··· |
|
| ··· |
| ··· |
|
| ··· |
（1）求
与
之间的函数关系式；
（2）当摄氏温度为零下
时，求华氏温度为多少？
