Question

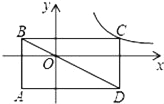
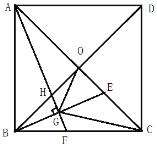
【题目】如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点（不与O、C重合），作AF⊥BE，垂足为G，分别交BC、OB于F、H，连接OG、CG.

（1）求证：AH=BE；

（2）∠AGO的度数是否为定值？说明理由；

（3）若∠OGC=90°，BG=，求△OGC的面积.

Answer 1

【答案】（1）详见解析；（2）∠AGO =45°；（3）S△COG =3.

【解析】

(1)根据正方形的性质，证≌，即可得出结论；

(2)根据及正方形的性质可得∽，根据相似比可得，又，可证∽，则，即可得出结论；

(3)根据∽，可证，，则，由(2)中结论可证，则∽，，即可得.

解：(1)∵四边形是正方形，

∴，

∵，

∴，

∴，

∴≌，

∴;

(2)∵，

∴∠BAH=∠FBG，

∵∽，

∴，

∴，

∵，

∴∽，

∴，

即的度数为定值.

(3)∵，

∴，

∵∽，

∴，

∴，

∵，，

∴，

∴∽，

∴，

∴，

∴.