题目内容
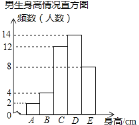
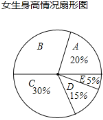
【题目】某校为了了解学生的身高情况，随机对该校男生、女生的身高进行抽样调查，已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制成下面的统计图表：
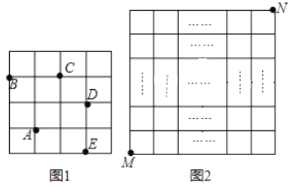
组别 | A | B | C | D | E |
身高（cm） | x＜150 | 150≤x＜155 | 155≤x＜160 | 160≤x＜165 | x≥165 |
根据图表中信息，回答下列问题：
（1）在样本中，男生身高的中位数落在 组（填组别序号），女生身高在B组的人数有 人；
（2）已知该校共有男生500人，女生480人，请估计身高在155≤x＜165之间的学生约有多少人？
（3）从男生样本的A、B两组里，随机安排2人参加一项活动，求恰好是1人在A组、1人在B组的概率．
【答案】（1）D；12 （2）541人 （3）
【解析】
（1）先求出调查的男生总人数，然后根据中位数的定义即可得出结论，根据调查的男生总人数和女生总人数相同，并求出女生身高在B组的人数所占调查的女生人数的百分比即可求出结论；
（2）分别求出C组中的男生人数和女生人数，求和即可；
（3）根据题意，列出表格，然后结合概率公式求概率即可．
解：（1）调查的男生总人数为2＋4＋12＋14＋8=40（人）
由条形统计图可得：男生身高的中位数落在D组，
∵抽取的样本中，男生、女生的人数相同，
∴调查的女生总人数为40人
女生身高在B组的人数有40×（1－20%－30%－15%－5%）=12（人）
故答案为：D；12；
（2）500×
＋480×（30%＋15%）=325＋216=541（人）
答：估计身高在155≤x＜165之间的学生约有541人；
（3）设A组的两个男生表示为A1、A2，B组的四个男生表示为B1、B2、B3、B4，列表如下：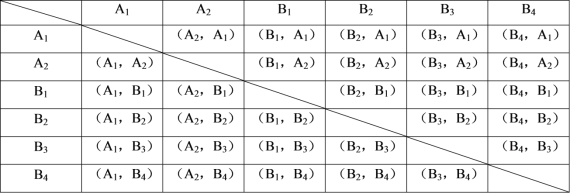
由表格可知：共有30种等可能的结果，其中恰好是1人在A组、1人在B组的结果有16种
∴恰好是1人在A组、1人在B组的概率为16÷30=．
【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品，成本价8元/千克，经过市场调查，该产品的日销售量
（千克）与销售单价
（元/千克）之间满足一次函数关系，该产品的日销售量与销售单价几组对应值如表：
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
（注：日销售利润
日销售量
（销售单价
成本单价）
（1）求关于的函数解析式（不要求写出的取值范围）；
（2）根据以上信息，填空：
①
_______千克；
②当销售价格
_______元时，日销售利润
最大，最大值是_______元；
（3）该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象，为了保证捐赠后每天的剩余利润不低于1500元，试确定该产品销售单价的范围．
