题目内容
【题目】某养殖户长期承包一口鱼糖养鱼，每年养殖一批，从鱼苗放入养到成品需要300天，鱼糖承包费用每年5000元，他记录了前几年平均每天投入饲料量（单位：kg）与年底成品鱼（达到一定规格可以销售）产量之间的关系如下表：
平均每天投入饲料（kg） | 20 | 25 | 30 | 40 | 50 | 60 | 70 | 80 |
成品鱼产量（kg） | 2800 | 3000 | 3200 | 3600 | 3900 | 4000 | 3900 | 3600 |
（1）请用适当的函数模型描述平均每天投入饲料数量与成品鱼产量之间的关系；
（2）如果今年的饲料价格为1．6元/kg，成品鱼销售价为20元/kg，鱼苗费用4000元，假设养成的成品鱼全部都能按此价格卖出．请建立适当的函数模型平均每天投入饲料多少千克时，该养殖户当年在该鱼糖养殖这种鱼获得的利润最多，最多利润是多少元？（利润＝销售收入﹣饲料成本﹣鱼糖承包费﹣鱼苗成本）．
【答案】（1）
；（2）平均每天投入饲料60千克时，该养殖户当年在该鱼糖养殖这种鱼获得的利润最多，最多利润是47200元．
【解析】
（1）分段函数：①20≤x≤40，是一次函数；②40≤x≤80，是二次函数；
（2）设利润为w，得出w与x之间的函数关系式，根据一次函数和二次函数的性质解答即可．
：（1）当20≤x≤40时，设y=kx+b，根据题意得：
，解得
；
当40≤x≤80时，设y=ax2+bx+c，根据题意的：
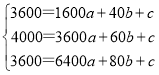，解得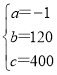
．
∴y＝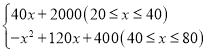
；
（2）设利润为w，根据题意得：
①当20≤x≤40时，w=20（40x+2000）-300×1.6x-5000-4000=320x+31000，
∵k＞0，∴w随x的增大而增大，∴当x=40时，w有最大值为：320×40+31000=43800（元）；
②当40≤x≤80时，y=-x2+120x+400，
∵对称轴x＝
＝60，函数有最大值y=4000；
4000×20-300×60×1.6-4000=47200（元）．
所以平均每天投入饲料60千克时，该养殖户当年在该鱼糖养殖这种鱼获得的利润最多，最多利润是47200元．
