Question

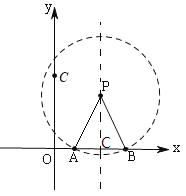
【题目】如图，在平面坐标系xOy中，点A的坐标为（1，0），点P的横坐标为2，将点A绕点P旋转，使它的对应点B恰好落在x轴上（不与A点重合）；再将点B绕点O逆时针旋转90°得到点C．

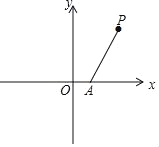
（1）直接写出点B和点C的坐标；

（2）求经过A，B，C三点的抛物线的表达式．

Answer 1

【答案】（1）点B的坐标为（3，0），点C的坐标为（0，3）；

（2）抛物线解析式为y＝x2﹣4x+3．

【解析】

（1）由题可知B点于A点关于直线对称，即可求解；B绕点O逆时针旋转90°得到点C，可得知C落在y的正半轴上，且距离O点的距离同B点一样，据此可得出C点的坐标；

（2）可把抛物线的解析式设成交点式，再代入已知点的坐标即可求解.

解：（1）如图所示，PA=PC，且PC所在的直线为

∴B点于A点关于直线对称

∴点B的坐标为（3，0），

∵B绕点O逆时针旋转90°得到点C

∴ C落在y的正半轴上，且距离O点的距离同B点一样

∴点C的坐标为（0，3），

（2）由题可设抛物线解析式为，

把（0，3）代入得：3a＝3，

解得：a＝1，

∴抛物线解析式为y＝x2﹣4x+3．