题目内容
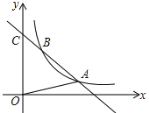
【题目】若二次函数y=ax2+bx﹣2的图象与x轴交于点A(4,0),与y轴交于点B,且过点C (3,﹣2).

(1)求二次函数表达式;
(2)若点P为抛物线上第一象限内的点,且S△PBA=5,求点P的坐标;
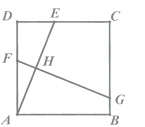
(3)在AB下方的抛物线上是否存在点M,使∠ABO=∠ABM?若存在,求出点M到y轴的距离;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,点M到y轴的距离为
;(3)存在,点M到y轴的距离为![]()
【解析】
(1)由待定系数法可求解析式;
(2)设直线BP与x轴交于点E,过点P作PD⊥OA于D,设点P(a,![]() a2-
a2-![]() a-2),则PD=
a-2),则PD=![]() a2-
a2-![]() a-2,利用参数求出BP解析式,可求点E坐标,由三角形面积公式可求a,即可得点P坐标;
a-2,利用参数求出BP解析式,可求点E坐标,由三角形面积公式可求a,即可得点P坐标;
(3)如图2,延长BM到N,使BN=BO,连接ON交AB于H,过点H作HF⊥AO于F,由全等三角形的性质和锐角三角函数求出点N坐标,求出BN解析式,可求点M坐标,即可求解.
(1)∵二次函数y=ax2+bx-2的图象过点A(4,0),点C (3,-2),
∴![]() ,
,
解得: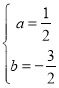
∴二次函数表达式为:![]() ;
;
(2)设直线BP与x轴交于点E,过点P作PD⊥OA于D,

设点P(a,![]() a2-
a2-![]() a-2),则PD=
a-2),则PD=![]() a2-
a2-![]() a-2,
a-2,
∵二次函数![]() 与y轴交于点B,
与y轴交于点B,
∴点B(0,-2),
设BP解析式为:![]() ,
,
∴![]() a2-
a2-![]() a-2=ka﹣2,
a-2=ka﹣2,
∴![]() ,
,
∴BP解析式为:y=(![]() )x﹣2,
)x﹣2,
∴y=0时,![]() ,
,
∴点E(![]() ,0),
,0),
∵S△PBA=5,
∵S△PBA=![]() ,
,
∴![]() ,
,
∴a=-1(不合题意舍去),a=5,
∴点P(5,3);
(3)如图2,延长BM到N,使BN=BO,连接ON交AB于H,过点H作HF⊥AO于F,
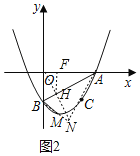
∵BN=BO,∠ABO=∠ABM,AB=AB,
∴△ABO≌△ABN(SAS)
∴AO=AN,且BN=BO,
∴AB垂直平分ON,
∴OH=HN,AB⊥ON,
∵AO=4,BO=2,
∴AB=![]() ,
,
∵S△AOB=![]() ×OA×OB=
×OA×OB=![]() ×AB×OH,
×AB×OH,
∴OH=![]() ,
,
∴AH= ,
,
∵cos∠BAO=![]() ,
,
∴ ,
,
∴AF=![]() ,
,
∴HF=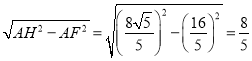 ,
,
OF=AO﹣AF= 4﹣![]() =
=![]() ,
,
∴点H(![]() ,-
,-![]() ),
),
∵OH=HN,
∴点N(![]() ,﹣
,﹣![]() )
)
设直线BN解析式为:y=mx﹣2,
∴﹣![]() =
=![]() m﹣2,
m﹣2,
∴m=﹣![]() ,
,
∴直线BN解析式为:y=﹣![]() x﹣2,
x﹣2,
∴![]() x2﹣
x2﹣![]() x﹣2=﹣
x﹣2=﹣![]() x﹣2,
x﹣2,
∴x=0(不合题意舍去),x=![]() ,
,
∴点M坐标(![]() ,﹣
,﹣![]() ),
),
∴点M到y轴的距离为![]() .
.

【题目】某宾馆有若干间标准房,当标准房的价格为![]() 元时,每天入住的国间数为
元时,每天入住的国间数为![]() 间,经市场调查表明,该宾馆每间标准房的价格在
间,经市场调查表明,该宾馆每间标准房的价格在![]() 元之间(含
元之间(含![]() 元,
元,![]() 元)浮动时,每天人住的房间数
元)浮动时,每天人住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| …… | 190 | 200 | 210 | 220 | …… |
| …… | 65 | 60 | 55 | 50 | …… |
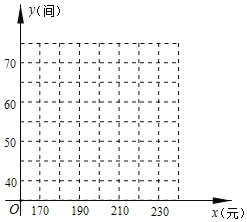
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)猜想(1)中的图象是什么函数的图象,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?