题目内容
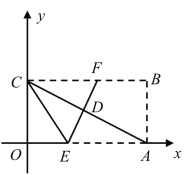
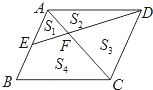
【题目】如图所示,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AD与AB的比等于( )
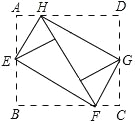
A. 25:24 B. 16:15 C. 5:4 D. 4:3
【答案】A
【解析】
先根据图形翻折的性质可得到四边形EFGH是矩形,再根据全等三角形的判定定理得出Rt△AHE≌Rt△CFG,再由勾股定理及直角三角形的面积公式即可解答.
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=90°,
∴∠HEF=90°,
同理四边形EFGH的其它内角都是90°,
∴四边形EFGH是矩形,
∴EH=FG(矩形的对边相等),
又∵∠1+∠4=90°,∠4+∠5=90°,
∴∠1=∠5(等量代换),
同理∠5=∠7=∠8,
∴∠1=∠8,
∴Rt△AHE≌Rt△CFG,
∴AH=CF=FN,
又∵HD=HN,
∴AD=HF,
在Rt△HEF中,EH=3,EF=4,根据勾股定理得HF=![]() =5,
=5,
又∵HEEF=HFEM,
∴EM=![]() ,
,
又∵AE=EM=EB(折叠后A、B都落在M点上),
∴AB=2EM=![]() ,
,
∴AD:AB=5:![]() =
=![]() =25:24.
=25:24.
故选:A

练习册系列答案
相关题目