题目内容
【题目】“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的关于x,y的二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1a2,把y2项系数c分解成两个因数c1,c2的积,即c=c1c2,并使a1c2+a2c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y).
例:分解因式:x2﹣2xy﹣8y2.
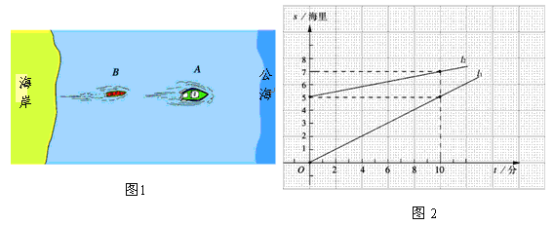
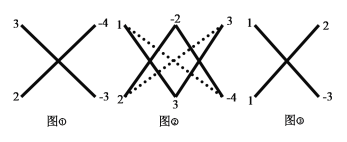
解:如图1,其中1=1×1,﹣8=(﹣4)×2,而﹣2=1×2+1×(﹣4).
∴x2﹣2xy﹣8y2=(x﹣4y)(x+2y)
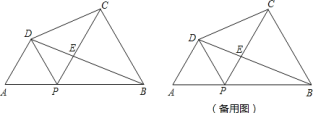
而对于形如ax2+bxy+cy2+dx+ey+f的x,y的二元二次式也可以用十字相乘法来分解,如图2,将a分解成mn乘积作为一列,c分解成pq乘积作为第二列,f分解成jk乘积作为第三列,如果mq+np=b,pk+qj=e,mk+nj=d,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式=(mx+py+j)(nx+qy+k);
例:分解因式:x2+2xy﹣3y2+3x+y+2
解:如图3,其中1=1×1,﹣3=(﹣1)×3,2=1×2;
而2=1×3+1×(﹣1),1=(﹣1)×2+3×1,3=1×2+1×1;
∴x2+2xy﹣3y2+3x+y+2=(x﹣y+1)(x+3y+2)
请同学们通过阅读上述材料,完成下列问题:
(1)分解因式:
①6x2﹣17xy+12y2=
②2x2﹣xy﹣6y2+2x+17y﹣12=
③x2﹣xy﹣6y2+2x﹣6y=
(2)若关于x,y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积,求m的值.
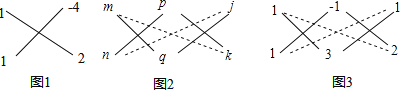
【答案】(1)①(3x﹣4y)(2x﹣3y),②(x﹣2y+3)(2x+3y﹣4),③(x﹣3y)(x+2y+2);(2)43或-78.
【解析】
(1)①参照图1,画出图形,根据十字相乘法则分解因式即可;
②参照图3,画出图形,根据十字相乘法则分解因式即可;
③参照图1,画出图形,根据十字相乘法则分解![]() ,再利用提取公因式法即可;
,再利用提取公因式法即可;
(2)参照图3,先根据所给的二元二次式画出图,然后根据十字相乘法则中对应系数的确认方法即可得.
(1)①如图①,其中![]() ,而
,而![]()
![]()
②如图②,其中![]()
而![]()
![]()
③如图③,其中![]() ,而
,而![]()
![]()
![]()
故答案为:①![]() ;②
;②![]() ;③
;③![]() ;
;
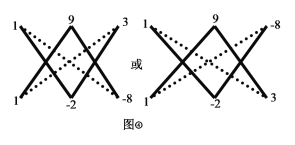
(2)如图④,由十字相乘法可知,有以下两种情况:
其中![]()
而![]()
![]() 或
或![]()
故m的值为![]() 或
或![]() .
.

【题目】已知二元一次方程![]() ,通过列举将方程的解写成下列表格的形式:
,通过列举将方程的解写成下列表格的形式:
| -1 |
|
| 5 | 6 |
| 6 | 5 |
| 0 |
|
如果将二元一次方程的解所包含的未知数![]() 的值对应直角坐标系中一个点的横坐标,未知数
的值对应直角坐标系中一个点的横坐标,未知数![]() 的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程
的值对应这个点的纵坐标,这样每一个二元一次方程的解,就可以对应直角坐标系中的一个点,例如:方程![]() 的解
的解![]() 的对应点是
的对应点是![]() .
.
(1)表格中的![]() ________,
________,![]() ___________;
___________;
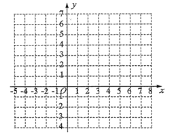
(2)通过以上确定对应点坐标的方法,将表格中给出的五个解依次转化为对应点的坐标,并在所给的直角坐标系中画出这五个点;根据这些点猜想方程![]() 的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
的解的对应点所组成的图形是_________,并写出它的两个特征①__________,②_____________;
(3)若点![]() 好落在
好落在![]() 的解对应的点组成的图形上,求
的解对应的点组成的图形上,求![]() 的值.
的值.