��Ŀ����
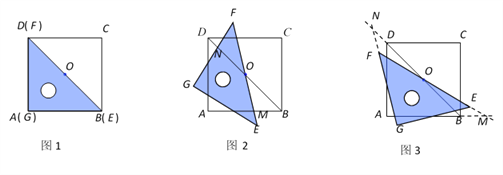
����Ŀ����1����ͼ1�����ı���ABCD�У���D=37������E��BC����һ�㣬��AE�۵�����B����AD��B��������B��E��CD�����B=_________����

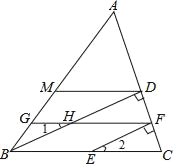
��2����ͼ2�����ı���ABCD�У�AB��CD����E��BC����һ�㣬��AE�۵�����B����AD��B��������F��BC����һ�㣬��DF�۵�����C����AD��C������B��E��C��F�к�λ�ù�ϵ��Ϊʲô��
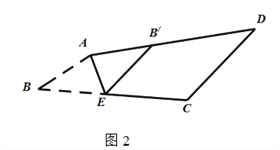
��3����ͼ3�����ı���ABCD�У���B=��D=90������E��BC����һ�㣬��AE�۵�����B����AD��B��������F��AD����һ�㣬��CF�۵�����D����BC��D���������ʣ�AE��CF�к�λ�ù�ϵ��˵�����ɣ�

��4�����ı���ABCD�У���E��BC����һ�㣬��AE�۵���
������B�����ı���ABCD��B��������ͼ4�������1����2����BAD����B֮���������ϵΪ________��
������B�����ı���ABCD��B��������ͼ5�������1����2����BAD����B֮���������ϵΪ ______��

���𰸡���1��37����2��B��E��C��F�����ɼ��⣻��3��AE��CF�����ɼ���������4���١�1+��2=��BAD+2��B��180�����ڡ�2����1=��BAD+2��B��180��
�����������������(1)������B��E��CD�ó���AB��E=��D=37�㣬Ȼ������۵�ͼ�ε����ʵó��𰸣�(2)������AB��CD�ó���B+��C=180�㣬�����۵�ͼ�εó���AB��E=��B����DC��F=��C��Ȼ�����ƽ�ǵ����ʵó���DC��F=��EB��C���Ӷ��ó��𰸣�(3)�����ݡ�B+��D=180���ó���BAD+��DCB=180�㣬Ȼ������۵�ͼ�ε����ʵó���BAE+��FCD��=90�㣬���ݡ�B�Ķ����ó���BAE+��AEB=90�㣬�Ӷ��õ���AEB=��FCD�䣬���ó�ƽ�У�(4)������ƽ���ߵ����ʡ��۵�ͼ�ε������Լ������ε��ڽǺͶ����ó�����֮��Ĺ�ϵ��
���������(1)����B��E��CD�� ���AB��E=��D=37�㣬�����۵�ͼ�Σ����B=��AB��E=37�㣻
(2)����AB��CD�����B+��C=180�㣬�����۵�ͼ�Σ� ���AB��E=��B����DC��F=��C��
���AB��E+��DC��F=180�㣬�ߡ�AB��E+��EB��C=180�㣬���DC��F=��EB��C��
��B��E��C��F��
(3)���ߡ�B+��D=180�㣬 ���BAD+��DCB=180�㣬
�����۵�ͼ�Σ� ���BAE+��FCD��=180���2=90�㣬�ߡ�B=90�㣬
���BAE+��AEB=90�㣬���AEB=��FCD�䣬��AE��FC��
(4)���١���1+��2=��BAD+2��B��180����
�ڡ���2����1=��BAD+2��B��180����