Question

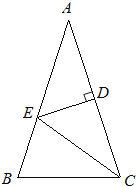
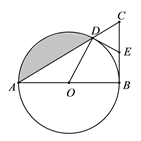
【题目】如图，△ABC中，∠ABC＝90°，以AB为直径的⊙O交AB于点D，点E为BC的中点，连接OD、DE．

⑴ 求证：OD⊥DE．

⑵ 若∠BAC＝30°，AB＝8，求阴影部分的面积．

Answer 1

【答案】

【解析】试题分析：（1）连接BD,易得BDC是直角三角形，E是中点，所以DE=BE，∠CBD=∠EDB,通过倒角知.

（2）用扇形面积减去三角形OAD面积就是阴影部分的面积，其中∠AOD是120°.

试题解析：

⑴ 连接DB.

∵ AB是⊙O的直径 ,

∴ ∠ADB＝90°,

∴ ∠CDB＝90°,

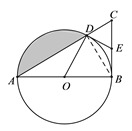
∵ 点E是BC的中点, ∴ DE＝CE＝,

∴ ∠EDC＝∠C，

∵ OA＝OD,∴ ∠A＝∠ADO,

∵ ∠ABC＝90°, ∠A＋∠C＝90° ，

∴ ∠ADO＋∠EDC＝90°，

∴ ∠ODE＝90°，

∴ OD⊥DE.

⑵∵∠BAC=30°，∠AOD=120°，

cm2，

∵AB＝8,AO=4， 勾股定理知AD=4，O到AD的距离是2，

，

∴ .