题目内容
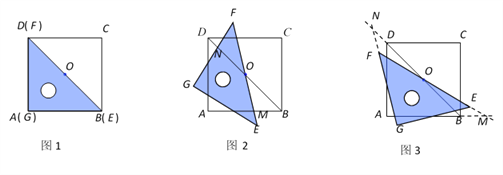
【题目】如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
【答案】(1)BM=FN,证明见解析;(2)BM=FN仍然成立,证明见解析.
【解析】试题分析:(1)根据正方形和等腰直角三角形的性质可证明△OBM≌△OFN,所以根据全等的性质可知BM=FN;
(2)同(1)中的证明方法一样,根据正方形和等腰直角三角形的性质得OB=OF,∠MBO=∠NFO=135°,∠MOB=∠NOF,可证△OBM≌△OFN,所以BM=FN.
试题解析:
(1)BM=FN.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠ABD=∠F=45°,OB=OF.
又∵∠BOM=∠FON,
∴△OBM≌△OFN.
∴BM=FN.
(2)BM=FN仍然成立.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠DBA=∠GFE=45°,OB=OF.
∴∠MBO=∠NFO=135°.
又∵∠MOB=∠NOF,
∴△OBM≌△OFN.
∴BM=FN.

练习册系列答案
相关题目