题目内容
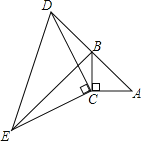
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AC=3,求BE的长度.
【答案】(1)证明见解析;(2)![]()
【解析】分析: (1)求出∠ACD=∠BCE,根据SAS推出两三角形全等即可;
(2)根据全等得出AD=BE,根据勾股定理求出AB,即可求出AD,代入求出即可.
本题解析:
证:(1)∵∠ACD=90°+∠BCD,∠BCE=90°+∠BCD
∴∠ACD=∠BCE
又∵AC=BC DC=EC∴△ACD≌△BCE
(2)∵BC=AC=3 △ACB是直角三角形
∴AB=3![]()
∴AD=2AB=6![]()
∵△ACD≌△BCE
∴BE=AD=6![]()
点睛:本题主要考查的知识点是:全等三角形的判定与性质.判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰直角三角形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】今年某区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设购买甲种树苗x棵,有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x的式子表示);
树苗类型 | 甲种树苗 | 乙种树苗 |
购买树苗数量(单位:棵) | x | |
购买树苗的总费用(单位:元) |
②如果购买甲、乙两种树苗共用去25 600元,那么甲、乙两种树苗各购买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26 000元,求n的最大值.