题目内容
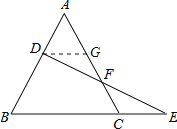
【题目】已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.
求证:AD=CE.

【答案】详见解析.
【解析】
过点D作DG∥BC交AC于G,先证明△DFG≌△EFC,根据全等三角形的对应边相等可得GD=CE,再证明△ADG是等边三角形,得出AD=GD,即可得出结论.
证明:过点D作DG∥BC交AC于G,如图所示:
则∠DGF=∠ECF,
在△DFG和△EFC中, ,
,
∴△DFG≌△EFC(AAS),
∴GD=CE,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∵DG∥BC,
∴∠ADG=∠B,∠AGD=∠ACB,
∴∠A=∠ADG=∠AGD,
∴△ADG是等边三角形,
∴AD=GD,
∴AD=CE.

练习册系列答案
相关题目
【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?