Question

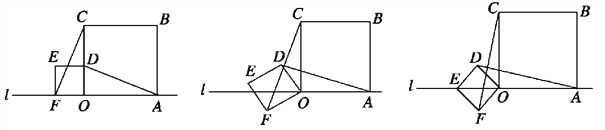
【题目】如图，在△ABC中，CD平分∠ACB交AB于点D，E为AC上一点，且DE∥BC

（1）求证：DE=CE；

（2）若∠A=90°，S△BCD=26，BC=13，求AD．

Answer 1

【答案】（1）详见解析；（2）4.

【解析】

（1）依据角平分线的定义以及平行线的性质，即可得到∠BCD=∠ECD=∠CDE，进而利用等角对等边判定DE=CE；

（2）过D作DF⊥BC于F，依据角平分线的性质，即可得到AD=FD，再根据S△BCD=26，即可得出DF得到长，进而得到AD的长．

解：（1）∵CD平分∠ACB，∴∠ECD＝∠BCD，又∵DE∥BC ∴∠BCD＝∠CDE.

∴∠ECD＝∠EDC ∴DE＝CE；

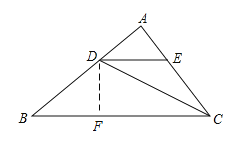
（2）如图，过D作DF⊥BC于F，

∵∠A＝90°，CD平分∠ACB，∴AD＝FD，

∵S△BCD＝26，BC＝13，∴ ×13×DF＝26，∴DF＝4，∴AD＝4．