��Ŀ����
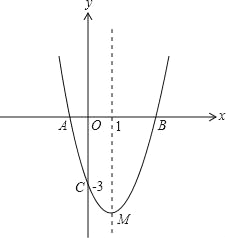
����Ŀ����11�֣���ͼ��������y=ax2+bx��3��x�ύ��A��B���㣬��y�ύ��C�㣬�Ҿ����㣨2����3a�����Գ�����ֱ��x=1��������M��
��1���������߶�Ӧ�ĺ�������ʽ��
��2������C��M������ֱ����x�ύ�ڵ�N�������������Ƿ���������ĵ�P��ʹ�Ե�P��A��C��NΪ������ı���Ϊƽ���ı��Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
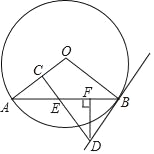
��3����ֱ��y=��x+3��y��Ľ�����D�����߶�BD����ȡһ��E������B��D�غϣ�������A��B��E�����Բ��ֱ��BC�ڵ�F�����ж���AEF����״����˵�����ɣ�
��4����E��ֱ��y=��x+3������һ��ʱ����3���еĽ����Ƿ��������ֱ��д�����ۣ���
���𰸡���1��y=x2��2x��3����2�����ڣ�P��2����3������3����AEF�ǵ���ֱ�������Σ����ɼ���������4����AEF�ǵ���ֱ�������Σ�
�������������������1���������������������a��b��ֵ��������������ʽ��
��2���ֱ���x=0��y=0���A��B��C��������꣬Ȼ������ֱ��CM�Ľ���ʽ��֤���ı���ANCPΪƽ���ı��ο������P�����ꣻ
��3�����ֱ��y=-x+3��������Ľ���D��B�����꣮Ȼ��֤����AFE=��ABE=45����AE=AF����֤��������AEF�ǵ���ֱ�������Σ�
��4�����ݣ�3���������ɵó���E��ֱ��y=-x+3������һ��ʱ����3���еĽ����Գ�����
���������(1)������������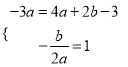 ��
��
���![]() ��
��
�������߶�Ӧ�ĺ�������ʽΪy=x22x3��
(2)����.����AP��CP��
����ͼ��ʾ��
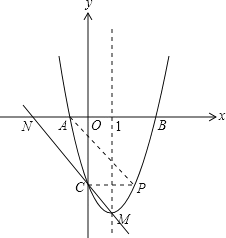
��y=x22x3����x=0����y=3.
��y=0����x22x3=0��
��x1=1��x2=3.
��A(1��0)��B(3��0)��C(0��3).
��y=(x1)24��
�ඥ��M(1��4)��
�������ֱ��CM�ı���ʽ��y=x3.
��y=x3����y=0����x=3.
��N(3��0)��
��AN=2��
��y=x22x3������y=3����x1=0��x2=2.
��CP=2��
��AN=CP.
��AN��CP��
���ı���ANCPΪƽ���ı�������ʱP(2��3)��
(3)��AEF�ǵ���ֱ��������.
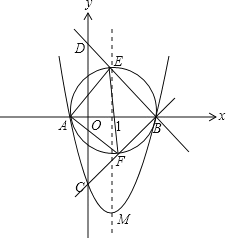
���ɣ���y=x+3�У���x=0����y=3����y=0����x=3.
��ֱ��y=x+3��������Ľ�����D(0��3)��B(3��0).
��OD=OB��
���OBD=45����
�֡ߵ�C(0��3)��
��OB=OC.
���OBC=45����
��ͼ֪��AEF=��ABF=45������AFE=��ABE=45����
���EAF=90������AE=AF.
���AEF�ǵ���ֱ�������Σ�
(4)����E��ֱ��y=x+3������һ��ʱ��(3)�еĽ��ۣ���AEF�ǵ���ֱ�������γ���.

����Ŀ��һ���ݽ������У���ί�����ݽ����ݡ��ݽ��������ݽ�Ч��������Ϊѡ�ִ�֣�����ɼ������ٷ��ƣ��������������ѡ�ֵĵ���ɼ����±���ʾ��
ѡ�� | �ݽ����� | �ݽ����� | �ݽ�Ч�� |
�� | 85 | 95 | 95 |
�� | 95 | 85 | 95 |
��1�������Ϊ��������ijɼ�ͬ����Ҫ�������ǵijɼ�����˭��ʤ����
��2��������ݽ�����ռ50%���ݽ�����ռ40%���ݽ�Ч��ռ10%�ı�������ס��ҵ�ƽ���ɼ�����ô˭��ʤ����