[题目]如图.已知Rt△ABC.∠C=90°．(1)求作:△ABC的内切圆⊙O,(尺规作图.不写作法.保留痕迹)(2)在(1)中.∠AOB的度数为．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，已知Rt△ABC，∠C=90°．

（1）求作：△ABC的内切圆⊙O；（尺规作图，不写作法，保留痕迹）

（2）在（1）中，∠AOB的度数为　　．

【答案】(1)见解析;(2) 135°.

【解析】分析：（1）首先由三角形的内心是三角形三个角平分线的交点，确定圆心，然后作边的垂线，确定半径，继而可求得△ABC的内切圆；

（2）根据三角形的内心是三角形三个角平分线的交点，由角平分线的性质和三角形的内角和求解..

详解：解：（1）如图，⊙O为所作；

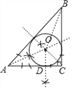
（2）∵点O为△ABC的内心，

∴OB平分∠ABC，OA平分∠BAC，

∴∠OBA=∠ABC，∠OAB=∠BAC，

∴∠OBA+∠OAB=（∠ABC+∠BAC）=×90°=45°，

∴∠AOB=180°﹣45°=135°．

故答案为135°．

练习册系列答案

（1）如图①，证明：BE＝BF．

（2）如图②，若∠ADC＝90°，O为AC的中点，G为EF的中点，试探究OG与AC的位置关系，并说明理由．

（3）如图③，若∠ADC＝60°，过点E作DC的平行线，并在其上取一点K（与点F位于直线BC的同侧），使EK＝BF，连接CK，H为CK的中点，试探究线段OH与HA之间的数量关系，并对结论给予证明．

【题目】如图，在菱形ABCD中，AB=2，∠DAB=60°,点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN.

（1）求证：四边形AMDN是平行四边形；

（2）填空：①当AM的值为时，四边形AMDN是矩形；②当AM的值为时，四边形AMDN是菱形。

【题目】如图，AB＝AC，BE⊥AC于点E，CF⊥AB于点F，BE，CF交于点D，则下列结论中不正确的是(　　)

A. △ABE≌△ACF B. 点D在∠BAC的平分线上

C. △BDF≌△CDE D. D是BE的中点

【题目】在正方形ABCD中，点E为对角线BD上一点，EF⊥AE交BC于点F，且F为BC的中点，若AB=4，则EF=_____．

【题目】[ 问题提出 ]

一个边长为 ncm(n3)的正方体木块，在它的表面涂上颜色，然后切成边长为1cm的小正方体木块，没有涂上颜色的有多少块？只有一面涂上颜色的有多少块？有两面涂上颜色的有多少块？有三面涂上颜色的多少块？

[ 问题探究 ]

我们先从特殊的情况入手

（1）当n=3时，如图（1）

没有涂色的：把这个正方形的表层“剥去”剩下的正方体，有1×1×1=1个小正方体；

一面涂色的：在面上，每个面上有1个，共有6个；

两面涂色的：在棱上，每个棱上有1个，共有12个；

三面涂色的：在顶点处，每个顶点处有1个，共有8个．

（2）当n=4时，如图（2）

没有涂色的：把这个正方形的表层“剥去”剩下的正方体，有2×2×2=8个小正方体：

一面涂色的：在面上，每个面上有4个，正方体共有个面，因此一面涂色的共有个；

两面涂色的：在棱上，每个棱上有2个，正方体共有条棱，因此两面涂色的共有个；

三面涂色的：在顶点处，每个顶点处有1个，正方体共有个顶点，因此三面涂色的共有个…

[ 问题解决 ]

一个边长为ncm(n3)的正方体木块，没有涂色的：把这个正方形的表层“剥去”剩下的正方体，有______个小正方体；一面涂色的：在面上，共有______个；两面涂色的：在棱上，共有______个；三面涂色的：在顶点处，共______个。

[ 问题应用 ]

一个大的正方体，在它的表面涂上颜色，然后把它切成棱长1cm的小正方体，发现有两面涂色的小正方体有96个，请你求出这个大正方体的体积．

【题目】直线y=﹣x+2与x轴、y轴分别交于点A、点C，抛物线经过点A、点C，且与x轴的另一个交点为B（﹣1，0）．

（1）求抛物线的解析式；

（2）点D为第一象限内抛物线上的一动点．

①如图1，若CD=AD，求点D的坐标；

②如图2，BD与AC交于点E，求S△CDE：S△CBE的最大值．

【题目】一个三位自然数m，将它任意两个数位上的数字对调后得一个首位不为0 的新三位自然数 m’（ m’可以与m相同），记m’=，在 m’ 所有的可能情况中，当|a+2b-c| 最小时，我们称此时的m’ 是m 的“幸福美满数”，并规定K (m) = a2 +2b2 -c2．例如：318按上述方法可得新数有：381、813 、138 ；因为|3+28－1｜＝ 18 ，｜8+ 21－3｜＝7，｜1 +23－8｜＝1，1< 7<18 ，所以138 是318的“幸福美满数”，K(318)=|12+232－82|=－45．

（1）若三位自然数t的百位上的数字与十位上的数字都为n（1≤n ≤ 9 ，n为自然数），个位上的数字为0 ，求证：K (t )＝ 0；

（2）设三位自然数s＝100+10x + y(1≤ x ≤ 9,1≤y≤9, ,x y 为自然数) ，且x<y ．交换其个位与十位上的数字得到新数s’，若19s+8s’=3888，那么我们称s为“梦

想成真数”，求所有“梦想成真数”中K (s )的最大值．

【题目】如图，菱形ABCD中，已知∠BAD=120°，∠EGF=60°, ∠EGF的顶点G在菱形对角线AC上运动，角的两边分别交边BC、CD于E、F．

[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]

（1）如图甲，当顶点G运动到与点A重合时，求证：EC+CF=BC；

（2）知识探究：

①如图乙，当顶点G运动到AC的中点时，请直接写出线段EC、CF与BC的数量关系（不需要写出证明过程）；

②如图丙，在顶点G运动的过程中，若，探究线段EC、CF与BC的数量关系；

（3）问题解决：如图丙，已知菱形的边长为8，BG=7，CF=，当＞2时，求EC的长度。

[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]

试题分类