题目内容
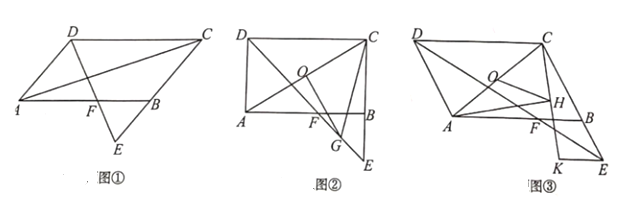
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
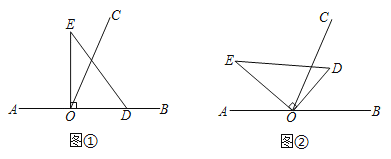
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
【答案】(1)详见解析;(2)GO⊥AC;(3)AH=![]() OH
OH
【解析】
(1)根据平行线的性质得出∠E=∠ADF,∠EFB=∠EDC,再利用ED平分∠ADC,即可解答
(2)连接BG,AG,根据题意得出四边形ABCD是矩形,再利用矩形的性质,证明△ABG≌△CEG,即可解答
(3)连接AK,BK,FK,先得出四边形BFKE是菱形,,再利用菱形的性质证明△KBE,△KBF都是等边三角形,再利用等边三角形的性质得出△ABK≌△CEK,最后利用三角函数即可解答
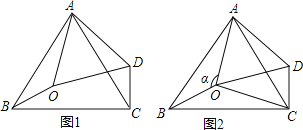
(1)证明:如图①中,因为四边形ABCD为平行四边形,
所以,AD∥EC,AB∥CD,
所以,∠E=∠ADF,∠EFB=∠EDC,
因为ED平分∠ADC,
所以,∠ADF=∠EDC,
所以,∠E=∠EFB,
所以,BE=BF
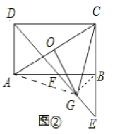
(2)解:如图⊙中,结论:GO⊥AC
连接BG,AG
∵四边形ABCD是平行四边形,∠ADC=90°,
四边形ABCD是矩形,
∠ABC=∠ABE=90°,
由(1)可知:BE=BF,
∵∠EBF=90°,EG=FG,
∴∠E=45°,∠GBF=∠GBE=45°,BG=GE=GF,
∵∠DCE=90°
∴∠E=∠EDC=45°,
∴DC=CE=BA,
∵∠ABG=∠E=45°,AB=EC,BG=EG,
∴△ABG≌△CEG(SAS),
∵GA=GC
∴AO=OC.
∴GO⊥AC
(3)解:如图⊙中,连接AK,BK,FK

∵BF=EK,BF∥EK,
∴四边形BFKE是平行四边形,
∵BF=BE,
∴四边形BFKE是菱形,
∵边形ABCD是平行四边形,
∴∠ADC=∠ABC=60°,∠DCB=∠DAB=120°
∴∠EBF=120°,
∴∠KBE=∠KBF=60°
BF=BE=FK=EK,
∴△KBE,△KBF都是等边三角形,
∴∠ABK=∠CEK=60°,∠FEB=∠FEK=30
∴∠CDE=∠CED=30°
∴CD=CE=BA,
∵BK=EK,
∴△ABK≌△CEK(SAS)
∴AK=CK,∠AKB=∠CKB
∴∠AKC=∠BKE=60°
∴△ACK是等边三角形
∵OA=OC,CH=HK
∴AK=2OH,AH⊥CK,
∴AH=AK·cos30°=![]() AK
AK
∴AH=![]() OH.
OH.