题目内容
【题目】[ 问题提出 ]
一个边长为 ncm(n3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块?
[ 问题探究 ]
我们先从特殊的情况入手
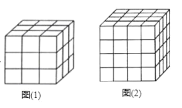
(1)当n=3时,如图(1)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体;
一面涂色的:在面上,每个面上有1个,共有6个;
两面涂色的:在棱上,每个棱上有1个,共有12个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
(2)当n=4时,如图(2)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:
一面涂色的:在面上,每个面上有4个,正方体共有 个面,因此一面涂色的共有 个;
两面涂色的:在棱上,每个棱上有2个,正方体共有 条棱,因此两面涂色的共有 个;
三面涂色的:在顶点处,每个顶点处有1个,正方体共有 个顶点,因此三面涂色的共有 个…
[ 问题解决 ]
一个边长为ncm(n3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有______个小正方体;一面涂色的:在面上,共有______个; 两面涂色的:在棱上,共有______个; 三面涂色的:在顶点处,共______个。
[ 问题应用 ]
一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积.
【答案】[ 问题探究 ] (2)6,24;12,24;8,8;[ 问题解决](n-2)3,(n-2)2,12(n-2),8;
[ 问题解决 ] 1000cm3.
【解析】
[ 问题探究 ] (2)根据(1)即可填写;
[ 问题解决 ] 可根据(1)、(2)的规律填写;
[ 问题应用 ] 根据[ 问题解决 ]知两面涂色的为![]() ,由此得到方程
,由此得到方程![]() =96,
=96,
解得n的值即可得到边长及面积.
[ 问题探究 ]
(2)没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:
一面涂色的:在面上,每个面上有4个,正方体共有 6个面,因此一面涂色的共有24个;
两面涂色的:在棱上,每个棱上有2个,正方体共有12 条棱,因此两面涂色的共有24个;
三面涂色的:在顶点处,每个顶点处有1个,正方体共有8 个顶点,因此三面涂色的共有8 个…
[ 问题解决 ]
一个边长为ncm(n3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有_![]() _____个小正方体;一面涂色的:在面上,共有__
_____个小正方体;一面涂色的:在面上,共有__![]() ____个; 两面涂色的:在棱上,共有__
____个; 两面涂色的:在棱上,共有__![]() ____个; 三面涂色的:在顶点处,共_8____个。
____个; 三面涂色的:在顶点处,共_8____个。
[ 问题应用 ]
由题意得,![]() =96,得n=10,
=96,得n=10,
∴这个大正方体的边长为10cm,
∴这个大正方体的体积为![]() (
(![]() ).
).

 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?