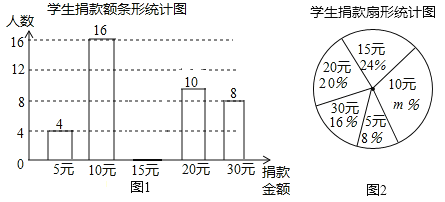
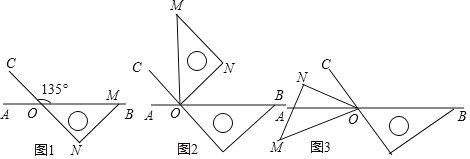
题目内容
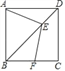
【题目】在正方形ABCD中,点E为对角线BD上一点,EF⊥AE交BC于点F,且F为BC的中点,若AB=4,则EF=_____.
【答案】![]()
【解析】分析:过点E作EM⊥AD于M,交BC于N,根据正方形的性质证得△AEM≌△EFN,然后全等三角形的性质,列方程求出FN、EN的长,最后根据勾股定理求得EF的长.
详解:过点E作EM⊥AD于M,交BC于N,如图,
∴四边形ABCD为正方形,
∴AD∥BC,∠BDM=45°,
∴MN=CD=4,ME=DM,
设ME=x,则DM=x,AM=4﹣x,NE=4﹣x,
∴AM=EN,
∵F为BC的中点,
∴FN=2﹣x,
∵EF⊥AE,
∴∠AEM=∠EFN,
在△AEM和△EFN中
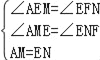 ,
,
∴△AEM≌△EFN,
∴ME=FN,即x=2﹣x,解得x=1,
∴FN=1,EN=3,
∴EF=![]() =
=![]() .
.
故答案为![]() .
.


练习册系列答案
相关题目