题目内容
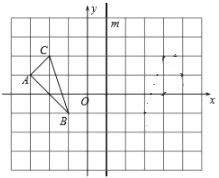
【题目】直线y=﹣x+2与x轴、y轴分别交于点A、点C，抛物线经过点A、点C，且与x轴的另一个交点为B（﹣1，0）．
（1）求抛物线的解析式；
（2）点D为第一象限内抛物线上的一动点．
①如图1，若CD=AD，求点D的坐标；
②如图2，BD与AC交于点E，求S△CDE：S△CBE的最大值．
【答案】（1）y=﹣x2+x+2；（2）①D（
，）；②S△CDE：S△CBE的最大值为
．
【解析】分析：（1）先求出A、C的坐标，再利用待定系数法求出函数的解析式；
（2）①根据等腰直角三角形的性质，确定点D的在y=x上，设出点D的坐标，代入y=﹣x2+x+2即可得到函数的解析式；
②作DF∥y轴交AC于F，BG∥y轴交直线AC于G，证得△DEF∽△BEG，然后根据相似三角形的面积比与相似比的关系，设出D点的坐标（t，﹣t2+t+2），再根据相似比的性质和二次函数的最值求解即可.
详解：（1）当x=0时，y=﹣x+2=2，则C（0，2），
当y=0时，﹣x+2=0，解得x=2，则A（2，0），
设抛物线解析式为y=a（x+1）（x﹣2），
把C（0，2）代入得a1（﹣2）=2，解得a=﹣1，
∴抛物线解析式为y=﹣（x+1）（x﹣2），
即y=﹣x2+x+2；
（2）①∵OA=OC，
∴△OAC为等腰直角三角形，
∵DC=DA，
∴点D在AC的垂直平分线上，
即点D在直线y=x上，
设D（m，m）（m＞0），
把D（m，m）代入y=﹣x2+x+2得﹣m2+m+2=m，解得m1=
，m2=﹣（舍去），
∴点D的坐标为（，）；
②作DF∥y轴交AC于F，BG∥y轴交直线AC于G，如图2，
∵DF∥BG，
∴△DEF∽△BEG，
∴
=
，
∵S△CDE：S△CBE=
，
∴S△CDE：S△CBE=，
当x=﹣1时，y=﹣x+2=3，则G（﹣1，3），
设D（t，﹣t2+t+2）（0＜t＜2），则F（t，﹣t+2），
∴DF=﹣t2+t+2﹣（﹣t+2）=﹣t2+2t，
∴S△CDE：S△CBE=
=
=﹣
（t﹣1）2+，
∴当t=1时，S△CDE：S△CBE的最大值为．
