��Ŀ����
�ڹ���202��·�Ľ������У�ij·�γ�4000�ף��ɼ����������̶�����30���ڣ���30�죩������ɣ���֪�������̶Ӹ���10�����ˣ�������������̶ӵĹ���ȫ���������������̶�ÿ��ÿ��Ĺ�������ͬ���ҹ��̶�ÿ��ÿ��Ĺ�������ͬ�������̶�1�졢�ҹ��̶�2�칲��·200�ף����̶�2�죬�ҹ��̶�3�칲��·350�ף�
��1�����ʼ����������̶�ÿ��ֱ���·�����ף�
��2�������������̶�ʩ��10������ڹ�����Ҫ��Ӽӳ��m��ȥѧϰ�¼������ܲ�Ҫ���ڹ涨ʱ������ɣ����ʼӿ��Գ�������ˣ�
��3����֪���̶�ÿ���ʩ������Ϊ0.6��Ԫ���ҹ��̶�ÿ���ʩ������Ϊ0.35��Ԫ��Ҫʹ�ù��̵�ʩ��������ͣ�������������������죿��ͷ���Ϊ���٣�
�⣺��1�����ÿ����·x�ף��Ҷ�ÿ����·y�ף�
��������ã�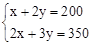 �����
�����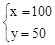 ��
��
�𣺼��̶�ÿ����·100�ף��ҹ��̶�ÿ����·50�ס�
��2����������ã�10��100+20��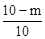 ��100+30��50��4000����ã�m��
��100+30��50��4000����ã�m��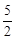 ��
��
��0��m��10����0��m��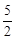 ��
��
��m����������m=1��2��
��ӿ��Գ��1�˻�2�ˡ�
��3������̶���a�죬�ҹ��̶���b�죬
��������ã�100a+50b=4000����b=80��2a��
��0��b��30����0��80��2a��30�����25��a��40��
�֡�0��a��30����25��a��30��
���ܷ���ΪWԪ����������ã�
W=0.6a+0.35b=0.6a+0.35��80��2a��=��0.1a+28��
�ߩ�0.1��0��
�൱a=30ʱ��W��С=��0.1��30+28=25����Ԫ����
��ʱb=80��2a=80��2��30=20���죩��
�𣺼��̶�����30�죬�ҹ��̶�����20�죬��ͷ���Ϊ25��Ԫ��
���������������1�����ÿ����·x�ף��Ҷ�ÿ����·y�ף�Ȼ�����������·�ij��ȷֱ�Ϊ200��350������������ϵ�г������飬Ȼ��ⷽ���鼴�ɵý⡣
��2�����ݼӳ��m�˺���������·�ij��Ȳ�С��4000�ף��г�һԪһ�β���ʽ��Ȼ�����m��ȡֵ��Χ���ٸ���m�����������
��3������̶���a�죬�ҹ��̶���b�죬��������·�ij���Ϊ4000���г�������������a��ʾ��b���ٸ���0��b��30��ʾ��a��ȡֵ��Χ���ٸ����ܷ��õ������ӵķ���֮����ʽ������Ȼ�����һ�κ����������Խ��

��ǿ����Ľ�Լ��ʶ������������Ȼ����Դ��ij����1��1������������ùܵ���Ȼ���۸���е�����ʵ�н���ʽ���ۣ���������շѼ۸������ʾ��
| ÿ�������� | ���ۣ�Ԫ/m3�� |
| ������75m3�IJ��� | 2.5 |
| ����75m3������125m3�IJ��� | a |
| ����125m3�IJ��� | a+0.25 |
��2�������ۺ�ÿ��֧����ȼ����Ϊy��Ԫ����ÿ�µ�������Ϊx��m3����y��x֮��Ĺ�ϵ��ͼ��ʾ����a��ֵ��y��x֮��ĺ�����ϵʽ��
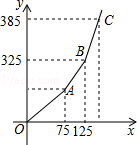
��3���ڣ�2���������£������û�2��3�·ݹ���1��175m3��3�·�����������2�·��������������ɷ�455Ԫ�����û�2��3�·ݵ����������Ƕ��٣�
���κ���y��ax2��bx��c(a��0)��ͼ����ͼ��ʾ����|ax2��bx��c|��k(k��0)����������ȵ�ʵ��������k��ȡֵ��Χ�ǣ� ��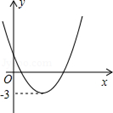
| A��k����3 | B��k����3 | C��k��3 | D��k��3 |
 ��ͼ����A��2��4����B����4��n�����㣮
��ͼ����A��2��4����B����4��n�����㣮




