��Ŀ����
��Rt��ABC�У���ACB=90�㣬BC=30��AB=50����P��AB��������һ�㣬ֱ��PE��AB�����AC�ཻ��E����ʱRt��AEP��Rt��ABC����M���߶�AP�ϣ���N���߶�BP�ϣ�EM=EN��EP:EM=12:13.
��1����ͼ1������E���C�غ�ʱ����CM�ij���
��2����ͼ2������E�ڱ�AC��ʱ����E�����A��C�غϣ���AP=x��BN=y����y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ.
��1��CM=26����2��y=50-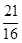 x��0<x<32
x��0<x<32
���������������1���ȸ�����֪�����ó�AC��ֵ���ٸ���CP��AB���CP���Ӷ��ó�CM��ֵ��
��2���ȸ���sin��EMP=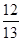 �����EP��ֵ���Ӷ��ó�EM��PM��ֵ���ٵó���AEP�ס�ABC���������
�����EP��ֵ���Ӷ��ó�EM��PM��ֵ���ٵó���AEP�ס�ABC���������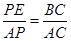 �����a��ֵ�����ɵó�y����x�ĺ�����ϵʽ�����������x��ȡֵ��Χ��
�����a��ֵ�����ɵó�y����x�ĺ�����ϵʽ�����������x��ȡֵ��Χ��
�⣺ ��1���ߡ�ACB=90�㣬
��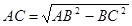
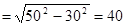 ��
��
��CP��AB��
��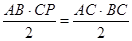
��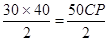 ��
��
��CP=24��
��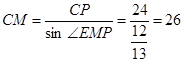 ��
��
��2����sin��EMP=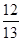 ��
��
����EP=12a����EM=13a��PM=5a��
��EM=EN��
��EN=13a��PN=5a��
�ߡ�AEP�ס�ABC��
��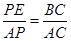 ��
��
��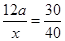 ��
��
��x=16a��
��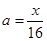 ��
��
��BP=50-16a��
��y=50-21a=50-21��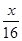 =50-
=50-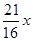
�ߵ�E����A���غ�ʱ��x=0����E����C���غ�ʱ��x=32��
��x��ȡֵ��Χ�ǣ���0��x��32��.
���㣺���������ε��ۺ���
���������������ѶȽϴ����п��бȽϳ�����һ����ѹ�����г��֣����ر�ע��.

Ϊ�������ǽ�Լ��ˮ����ʱ��©ˮ��ˮ��ͷ������ͬѧ�ֱ�����ˮ��ͷ©ˮʵ�飬�������ڽ�ˮ����Ͳ�������Ϊ100������
ʵ��һ��С��ͬѧ����ˮ��ͷ©ˮʵ��ʱ��ÿ��10��۲���Ͳ��ˮ���������¼�����������©����ˮ����ȷ��1��������
| ʱ��t���룩 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
| ©����ˮ��V�������� | 2 | 5 | 8 | 11 | 14 | 17 | 20 |

��2�����С��ͬѧ����ʵ�飬��̽����������Ͳ�е�ˮ�������������ȷ��1�룩��
��3������©ˮ�ٶȣ�һСʱ��©ˮ��������ǧ�ˣ���ȷ��0.1ǧ�ˣ�
ʵ�����
С��ͬѧ�����Լ���ʵ�����ݻ�����ͼ����ͼ2��ʾ��Ϊʲôͼ���л��������ᡰƽ�С��IJ��֣�

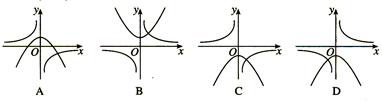
��֪���κ���y=ax2+bx+c��ͼ����ͼ����abc��0����b��a+c����4a+2b+c��0����2c��3b����a+b��m��am+b����m��1�������н�����ȷ���У�������
| A���ۢ� | B���ۢ� | C���ۢܢ� | D���ڢۢܢ� |
�����κ���y=x2��2x+c��ͼ����y��Ľ���Ϊ��0����3������˶��κ����У� ��
| A����СֵΪ-2 | B����СֵΪ-3 | C����СֵΪ-4 | D�����ֵΪ-4 |

 ����8��ʱ����ѩֹͣ������ʤ��ũ��ǰ��֧Ԯ������6�죬������˻�ũ�����е��ո�����ͼ1�ǻ�е�ո��Ķ��y1��Ķ�����˹��ո��Ķ��y2��Ķ����ʱ��x���죩֮��ĺ���ͼ��ͼ2��ʣ���ũ�����Ķ��w��Ķ����ʱ��x��֮��ĺ���ͼ������ͼ��ش��������⣮
����8��ʱ����ѩֹͣ������ʤ��ũ��ǰ��֧Ԯ������6�죬������˻�ũ�����е��ո�����ͼ1�ǻ�е�ո��Ķ��y1��Ķ�����˹��ո��Ķ��y2��Ķ����ʱ��x���죩֮��ĺ���ͼ��ͼ2��ʣ���ũ�����Ķ��w��Ķ����ʱ��x��֮��ĺ���ͼ������ͼ��ش��������⣮
 ��
��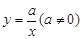 ��ͬһֱ������ϵ�е�ͼ������ǣ� ��
��ͬһֱ������ϵ�е�ͼ������ǣ� ��