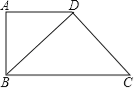
题目内容
【题目】已知△ABC为等边三角形，BD为△ABC的高，延长BC至E，使CE=CD=1，连接DE，则BE=___________，∠BDE=_________ ．
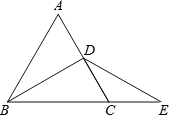
【答案】3 120°
【解析】
根据等腰三角形和30度角所对直角边等于斜边的一半，得到BC的长，进而得到BE的长，根据三角形外角性质求出∠E=∠CDE=30°，进而得出∠BDE的度数．
∵△ABC为等边三角形，∴∠ABC=∠ACB=60°，AB=BC．
∵BD为高线，∴∠BDC=90°，∠DBC
∠ABC=30°，
∴BC=2DC=2，∴BE=BC+CE=2+1=3．
∵CD=CE，∴∠E=∠CDE．
∵∠E+∠CDE=∠ACB=60°，∴∠E=∠CDE=30°，
∴∠BDE=∠BDC+∠CDE=120°．
故答案为：3，120°．
练习册系列答案
相关题目
