题目内容
【题目】如图,在梯形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC.
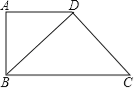
(1)△ABD与△DCB相似吗?请回答并说明理由;
(2)如果AD=4,BC=9,求BD的长.
【答案】(1)相似,解析见解析;(2)6.
【解析】
试题(1)由平行线的性质得∠ADB=∠DBC,已知∠BAD=∠BDC=90°,从而可得到△ABD∽△DCB.
(2)根据相似三角形的相似比即可求得BD的长.
试题解析:(1)△ABD与△DCB相似,理由如下:
∵AD∥BC,
∴∠ADB=∠DBC.
∵BD⊥DC,
∴∠BDC=90°.
∵∠BAD=90°,
∴∠BAD=∠BDC.
∴△ABD∽△DCB.
(2)∵△ABD∽△DCB,
∴![]()
∵AD=4,BC=9,
∴BD2=ADCB.
∴BD=6.

练习册系列答案
相关题目