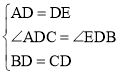Question

【题目】已知△ABC是等边三角形，P为△ABC所在平面内一个动点，BP=BA，若0°﹤∠PBC﹤ 180°，且∠PBC的平分线上一点D满足DB=DA.

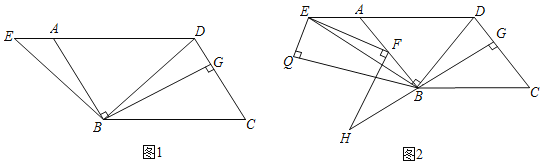
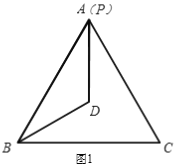
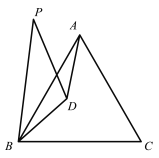
(1)当BP和BA重合时(如图1)，则∠BPD=______°.

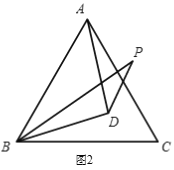
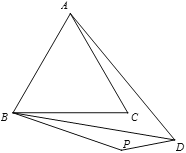
(2)当BP在∠ABC内部时(如图2)，求∠BPD的度数

(3)当BP在∠ABC外部时，请直接写出∠BPD的度数，并画出相应的图形.

Answer 1

【答案】(1)30；(2)∠BPD=30°；(3)图形见解析，∠BPD=30°或150°.

【解析】

（1）由于P，A重合，DP=DB，∠DBP=∠DPB，因为DB是∠PBC的平分线，因此，∠DBP=∠DPB=30°；
（2）本题可通过构建全等三角形来求解．连接CD，BP=BC，BD又是∠PBC的平分线，三角形PBD和三角形CBD中又有一公共边，因此两三角形全等，∠BPD=∠BCD，那么关键是求∠BCD的值，那么我们就要看∠BCD和∠ACB的关系了，可通过证明三角形ACD和BCD全等来得出，这两个三角形中，BD=AD，BC=AC，有一条公共边CD因此∠BCD=∠ACD=30°，那么就求出∠BPD的度数了；
（3）同（2）的证法完全一样，步骤有2个，一是得出∠BCD的度数，二是证明三角形BPD和BCD全等，同（2）完全一样．
（当∠BPD是钝角时，∠BPD=∠BCD=（360-60）÷2=150°，还是用的（2）中的三角形BPD，BCD全等，BCD，ACD全等）

解：(1)30°

(2)连结CD

∵ D在∠PBC的平分线上

∴∠PBD=∠CBD

∵△ABC是等边三角形

∴BA=BC=AC，∠ACB=60°

∵BP=BA

∴BP=BC

∵BD=BD

∴△PBD≌△CBD(SAS)

∴∠BPD=∠BCD

∵DB=DA，BC=AC，CD=CD

∴△BCD≌△ACD

∴∠BCD=∠ACD=∠ACB=30°

∴∠BPD=30°

(3)∠BPD=30°或150°