Question

【题目】在四边形中，，

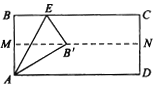
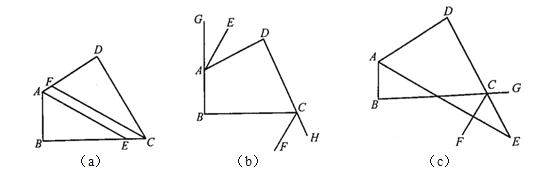
（1）如图(a)所示，、分别是和的角平分线，判断与的位置关系，并证明．

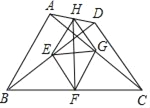
（2）如图(b)所示，、分别是和的角平分线，直接写出与的位置关系．

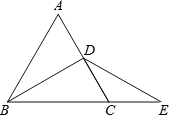
（3）如图(c)所示，、分别是和的角平分线，判断与的位置关系，并证明．

Answer 1

【答案】（1），证明见解析；（2）；（3），证明见解析

【解析】

（1）先根据四边形的内角和、角平分线的定义得出，再根据直角三角形的两锐角互余可得，从而可得，然后根据平行线的判定即可得；

（2）先由四边形的内角和得出，再根据角平分线的定义、邻补角的定义得出，然后根据等量代换、直角三角形的两锐角互余可得出，即，最后根据平行线的判定即可得；

（3）先根据四边形的内角和、邻补角的定义得出，再根据角平分线的定义得出，然后根据三角形的内角和定理得出，从而可得出．

（1）．证明过程如下：

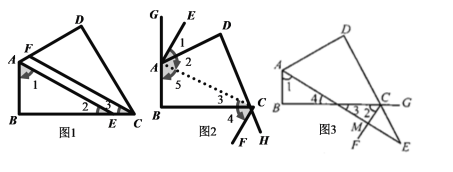
如图1，∵

∴

又∵、分别是、的角平分线

∴

∵

∴

∴；

（2）．证明过程如下：

如图2，连接AC

由（1）知，

是的角平分线

同理可得：

即

又，即

，即

；

（3）．证明过程如下：

如图3，设与相交于点

由（1）知，

∵

∴

∵、分别是和的角平分线

∴，

∴

∵

∴

∴．