Question

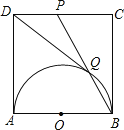
【题目】已知抛物线W：y=x-4x+2的顶点为A，与x轴交于点B、C.

（1）求∠ABC的正切值；

（2）若点P是抛物线W上的一点，过P作直线PQ垂直x轴，将抛物线W关于直线PQ对称，得到抛物线Wˊ，设抛物线Wˊ的顶点Aˊ，问：是否存在这样的点P，使得△APAˊ为直角三角形？若存在，求出对称所得的抛物线Wˊ的表达式；若不存在，请说明理由.

Answer 1

【答案】（1）.

【解析】

（1）如图，设对称轴与x轴交点为D，令y=0，可求出A、B两点坐标，可得BD的长，把抛物线解析式变成顶点式可得顶点坐标，可得AD的长，根据正切的定义求出叫ABC的正切值即可；（2）如图，设P（a，a2-4a+2），对称轴x=a与AA′交于E，由（1）可知原抛物线对称轴为直线x=2，A点坐标为（2，-2），当a>2时，由抛物线W与W′关于x=a对称，且∠APA′=90°，可得△APA′是等腰直角三角形，根据等腰直角三角形性质可得PE=AE，即可求出a的值，进而可得A′点坐标，根据顶点式即可得抛物线W′的解析式；同理可求出当a<2时抛物线W′的解析式.

（1）如图，设对称轴与x轴交点为D，

令y=0，则x2-4x+2=0，

解得x1=2-，x2=2+，

∴B点坐标为（2-，0），C点坐标为（2+，0），

∵y=x2-4x+2=(x-2)2-2，

∴顶点坐标为（2，-2），对称轴为直线x=2，

∴D点坐标为（2，0），

∴BD=，AD=2，

∴tan∠ABC===.

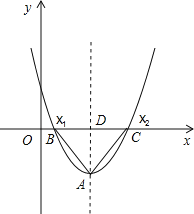
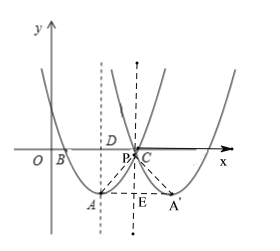
（2）如图，设P（a，a2-4a+2），对称轴x=a与AA′交于E，

①当a>2时，A（2，-2），E（a，-2），

∵抛物线W与抛物线W′关于直线x=a对称，∠APA′=90°，

∴△APA′是等腰直角三角形，

∴PE=AE，即a2-4a+2-(-2)=a-2，

解得：a1=2(舍去)，a2=3，

∴AE=3-2=1，

∴A′点的横坐标为3+1=4，

∴A′坐标为（4，-2），

∴抛物线W′的解析式为y=(x-4)2-2.

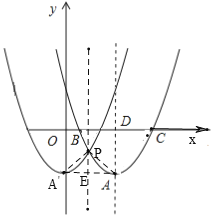
②如图，当a<2时，同理，PE=AE，

∴a2-4a+2-(-2)=2-a，

解得a1=2(舍去)，a2=1，

∴AE=2-1=1，

∴A′点的横坐标为1-1=0，

∴A′点坐标为（0，-2），

∴抛物线W′的解析式为y=x2-2.

综上所述：抛物线W′的解析式为y=(x-4)2-2或y=x2-2.