Question

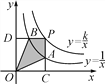
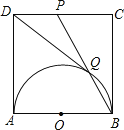
【题目】如图，正方形ABCD边长为1，以AB为直径作半圆，点P是CD中点，BP与半圆交于点Q，连接给出如下结论：；；；其中正确的结论是______填写序号

Answer 1

【答案】

【解析】

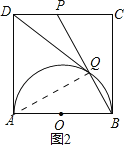
①连接OQ，OD，如图1．易证四边形DOBP是平行四边形，从而可得DO∥BP．结合OQ＝OB，可证到∠AOD＝∠QOD，从而证到△AOD≌△QOD，则有DQ＝DA＝1；

②连接AQ，如图2，根据勾股定理可求出BP．易证Rt△AQB∽Rt△BCP，运用相似三角形的性质可求出BQ，从而求出PQ的值，就可得到 的值；

③过点Q作QH⊥DC于H，如图3．易证△PHQ∽△PCB，运用相似三角形的性质可求出QH，从而可求出S△DPQ的值；

④根据图1和①中的结论可作判断．

①连接OQ，OD，如图1．

易证四边形DOBP是平行四边形，从而可得DO∥BP，

∴∠AOD＝∠OBP，∠DOQ＝∠OQB，

∵OB＝OQ，

∴∠OBP＝∠OQB，

∴∠AOD＝∠QOD，从而证到△AOD≌△QOD，

则有DQ＝DA＝1；

故①正确；

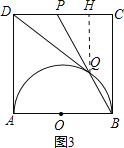
②连接AQ，如图2．

∵P是CD的中点，

∴CP＝CD＝，BP ．

易证Rt△AQB∽Rt△BCP，

∴，即，

∴BQ＝，

则PQ＝BP﹣BQ＝﹣＝，

∴＝ ；

故②正确；

③过点Q作QH⊥DC于H，如图3．

易证△PHQ∽△PCB，

∴ ，即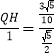

∴QH＝ ，

∴S△DPQ＝DPQH＝．

故③错误；

④如图1，由①知：△AOD≌△QOD，

∴∠ADQ＝2∠ODQ，

∵OD∥PB，

∴∠ODQ＝∠DQP，

∴∠ADQ＝2∠DQP，

故④正确，

综上所述：正确结论是①②④．

故答案为：①②④．