题目内容
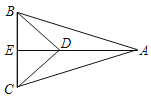
【题目】如图，Rt△ABO的顶点A是反比例函数y=
与一次函数y=﹣x﹣（k+1）的图象在第二象限的交点，AB⊥x轴于B，且S△ABO=
．
（1）直接写出这两个函数的关系式；
（2）求△AOC的面积；
（3）根据图象直接写出：当x为何值时，反比例函数的值小于一次函数的值．
【答案】（1）y=
；y=﹣x+2；（2）4；（3）x＜﹣1或0＜x＜3时；
【解析】
（1）先根据反比例函数的图象所在的象限判断出k的符号，在由△ABO的面积求出k的值，进而可得出两个函数的解析式；
（2）把两函数的解析式组成方程组，求出x、y的值，即可得出A、C两点的坐标，再由一次函数的解析式求出直线与x轴的交点，由S△AOC=S△AOD+S△COD进行解答即可．
（3）直接根据一次函数与反比例函数的交点坐标求出一次函数的值大于反比例函数的值x的取值范围即可．
解：（1）设点A（x，y），则xy=k
∵S△AOB=
∴
（﹣x）×y=
∴k=﹣3
∴反比例函数解析式y=
一次函数解析式y=﹣x+2
（2）由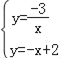
解得
，
∴A（﹣1，3）、C（3，﹣1）
∵一次函数y=﹣x+2与y轴的交点坐标为（0，2）
∴S△AOC=
×2×（3+1）=4
（3）由图象可得：当x＜﹣1或0＜x＜3时，一次函数图象在反比例图象的上方．
【题目】武胜县白坪—飞龙乡村旅游度假村橙海阳光景点组织
辆汽车装运完
三种脐橙共
吨到外地销售.按计划，辆汽车都要装运，每辆汽车只能装运同一种脐橙，且必须装满.根据下表提供的信息，解答以下问题：
脐橙品种 |
|
|
|
每辆汽车运载量（吨） |
|
|
|
每吨脐橙获得（元） |
|
|
|
设装运
种脐橙的车辆数为
，装运
种脐橙的车辆数为
，求与之间的函数关系式；
如果装运每种脐橙的车辆数都不少于
辆，那么车辆的安排方案有几种？
设销售利润为
（元），求与之间的函数关系式；若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润的值.
