题目内容
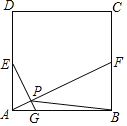
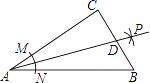
【题目】如图，在Rt△ABC中，∠C=90°，以A为圆心，以任意长为半径画弧，分别交AC、AB于点M、N，再分别以点M、N为圆心，以大于
MN的长为半径画弧，两弧相交于点P，作射线AP交BC于点D，若AC=4，BC=3，则CD的长为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
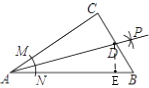
过D作DE⊥AB于E，由题意可知，AP为∠BAC的角平分线，根据角平分线性质打开CD=DE，利用勾股定理可求出AB的长，根据S△ABC=S△ACD+S△ADB即可求出CD的长.
过D作DE⊥AB于E，
∵∠C=90°，AC=4，BC=3，
∴AB=
=5，
由题意得：AP是∠BAC的角平分线，
∵∠C=90°，DE⊥AB，
∴CD=DE，
∵S△ABC=S△ACD+S△ADB
∴
AC
BC=CDAC+ABDE，即×4×3=×4CD+×5CD，
解得：CD=
.
故选B.
练习册系列答案
相关题目
