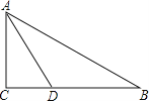
题目内容
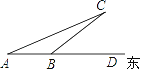
【题目】如图，在
中，
，点D在边
上，
，
，点D到
的距离为3，下列说法中：①
是
的平分线；②
是等腰三角形；③点D在的中垂线上；④
:
:3，其中说法正确的是 ______ 
把所有正确结论的序号都写在横线上)
【答案】①②③④
【解析】
在Rt△ACD中，由∠CAD=30°，AD=6，可得CD的长、∠ADC的度数，过点D作DE⊥AB，垂足为E，由点D到AB的距离与CD的大小关系，利用角平分线的判定定理，可判断①；由∠ADC、∠BAD间关系，可判断②；由等腰三角形及DE⊥AB，可判断③；根据高相等时，三角形的面积比等于底边的比可判断④．
解：过点D作
，垂足为，则
．
在
中，
，
，
，
．
，，
，
是
的平分线，故①正确；
，又
，
，
，
是等腰三角形，故②正确；
，，
是
的垂直平分线
点D在的中垂线上，故③正确；
，
:
:
:
:3，故④正确．
故答案为：①②③④．
练习册系列答案
阅读快车系列答案
相关题目
【题目】王勇和李明两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了30次实验，实验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
（1）分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率；
（2）王勇说：“根据以上实验可以得出结论：由于5点朝上的频率最大，所以一次实验中出现5点朝上的概率最大”；李明说：“如果投掷300次，那么出现6点朝上的次数正好是30次”．试分别说明王勇和李明的说法正确吗？并简述理由；
（3）现王勇和李明各投掷一枚骰子，请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．