题目内容
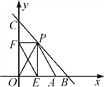
【题目】如图,直线y=-x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y=-x+10在第一象限内的一个动点.
(1)求△OPA的面积S与x的函数解析式,并写出自变量x的取值范围;
(2)过点P作PE⊥x轴于点E,作PF⊥y轴于点F,连接EF,是否存在一点P使得EF的长最小,若存在,求出EF的最小值;若不存在,请说明理由.
【答案】(1) S=40-4x(0<x<10);(2)存在点P使得EF的长最小,最小值为5![]()
【解析】试题分析:(1)利用三角形面积公式,得到S△OPA面积,得到S和x的关系.
(2) 四边形OEPF为矩形,OP垂直于BC时,OP最小,EF也最小.
试题解析:
解:(1)S△OPA=![]() OA·y=
OA·y=![]() ×8×(-x+10)=40-4x.
×8×(-x+10)=40-4x.
∴S=40-4x(0<x<10).
(2)存在点P使得EF的长最小,
∵四边形OEPF为矩形,
∴EF=OP,∴OP⊥BC时,OP最小,即EF最小.
∵B(10,0),C(0,0),∴OB=OC=10,BC=10![]() ..
..
∴OP=![]() =5
=5![]() ..
..
∴EF的最小值为5![]() .
.

【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
【题目】某射击教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填“变大”、“变小”或“不变”)