题目内容
【题目】![]() 是
是![]() 的直角三角形,
的直角三角形,![]() 的中点分别是点
的中点分别是点![]() 点
点![]() ,动点
,动点![]() 从点
从点![]() 出发,按箭头方向通过
出发,按箭头方向通过![]() 到
到![]() ;以
;以![]() 的速度运动,设
的速度运动,设![]() 点从
点从![]() 开始运动的距离为
开始运动的距离为![]() ,
,![]() 的面积为
的面积为![]() 试回答以下问题:
试回答以下问题:
(1)![]() 点从
点从![]() 出发到
出发到![]() 停止,写出
停止,写出![]() 与
与![]() 的函数关系式并写出
的函数关系式并写出![]() 的取值范围.
的取值范围.
(2)求出![]() 点从
点从![]() 出发后几秒时,
出发后几秒时,![]()

【答案】(1)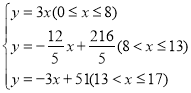 ;(2)点P从点B出发2秒或15秒时,
;(2)点P从点B出发2秒或15秒时,![]()
【解析】
(1)利用勾股定理求出AC,根据中点的性质求出CN、MN,再根据点P在BC边上,CN边上和MN边上时,分别求出函数解析式;
(2)先求出△ABC的面积根据![]() 求出△ABP的面积,再分别代入函数解析式,解出符合取值范围的x值即是答案.
求出△ABP的面积,再分别代入函数解析式,解出符合取值范围的x值即是答案.
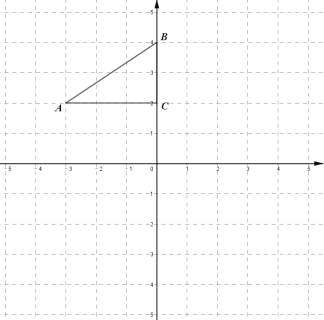
(1)在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() 的中点分别是点
的中点分别是点![]() 点
点![]() ,
,
∴CN=![]() AC=5,MN=
AC=5,MN=![]() BC=4,
BC=4,
当点P在BC边上即![]() 时,BP=x,∴
时,BP=x,∴![]() ;
;
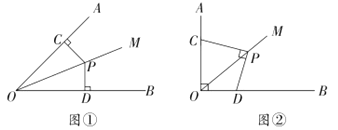
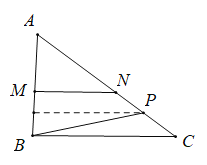
当点P在CN边上即![]() 时,如图:过点P作PH⊥AB于H,连接BP,
时,如图:过点P作PH⊥AB于H,连接BP,
∴∠AHP=∠B=90°,
∴HP∥BC,
∴∠APH=∠C,
∵AP=18-x,cos∠C=![]() ,
,
∴HP=![]() ,
,
∴![]() ;
;
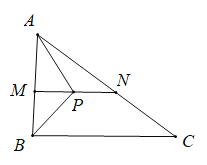
当点P在MN边上即![]() 时,如图:MP=17-x,
时,如图:MP=17-x,
∴![]()
综上,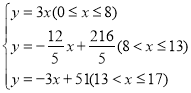 ;
;
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 时,3x=6,解得x=2,符合题意;
时,3x=6,解得x=2,符合题意;
当![]() 时,
时,![]() ,解得x=15.5>13,舍去;
,解得x=15.5>13,舍去;
当![]() 时,
时,![]() ,解得x=15,符合题意,
,解得x=15,符合题意,
∴点P从点B出发2秒或15秒时,![]() .
.

【题目】某商贸公司有![]() 、
、![]() 两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
体积(立方米/件) | 质量(吨/件) | |
| 0.8 | 0.5 |
| 2 | 1 |
(1)已知一批商品有![]() 、
、![]() 两种型号,体积一共是20立方米,质量一共是10.5吨,求
两种型号,体积一共是20立方米,质量一共是10.5吨,求![]() 、
、![]() 两种型号商品各有几件?
两种型号商品各有几件?
(2)物资公司现有可供使用的货车每辆额定载重3.5吨,容积为6立方米,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
现要将(1)中商品一次或分批运输到目的地,如果两种收费方式可混合使用,商贸公司应如何选择运送、付费方式,使其所花运费最少,最少运费是多少元?