题目内容
【题目】已知![]() 是
是![]() 的平分线,点
的平分线,点![]() 是射线
是射线![]() 上一点,点C、D分别在射线
上一点,点C、D分别在射线![]() 、
、![]() 上,连接PC、PD.
上,连接PC、PD.
(1)发现问题
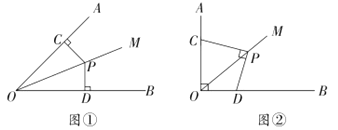
如图①,当![]() ,
,![]() 时,则PC与PD的数量关系是________.
时,则PC与PD的数量关系是________.
(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当![]() 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
时,PC与PD在(1)中的数量关系还成立吗?说明理由.
【答案】(1)PC=PD;(2)PC=PD仍然成立.理由见解析.
【解析】
(1)根据角平分线的性质可得出PC=PD;
(2)过P分别作PE⊥OB于E,PF⊥OA于F,由角平分线的性质得PE=PF,然后根据同角的补角相等得出∠FCP=∠PDE,即可由AAS证明△CFP≌△DEP,从而得证.
解:(1)∵OM是∠AOB的平分线,PC⊥OA,PD⊥OB,
∴PC=PD,
故答案为:PC=PD;
(2)PC=PD仍然成立.理由如下:
过P分别作PE⊥OB于E,PF⊥OA于F,
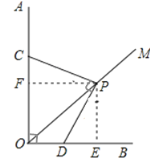
∴∠CFP=∠DEP=90°,
∵OM是∠AOB的平分线,∴PE=PF.
∵∠OCP+∠ODP=180°,又∠ODP+∠PDE=180°,
∴∠OCP=∠PDE,即∠FCP=∠PDE,
在△CFP和△DEP中,
 ,
,
∴△CFP≌△DEP(AAS),
∴PC=PD.

练习册系列答案
相关题目