题目内容
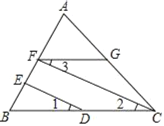
【题目】已知,如图,在ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形:
(2)若菱形ABEF的周长为16,∠BEF=120°,求AE的大小.

【答案】(1)详见解析;(2)4.
【解析】
(1)先证明四边形ABEF是平行四边形,再证明邻边相等即可证明.
(2)由菱形的对角线平分对角和等边三角形的判定推知△ABE是等边三角形,则AE=AB.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EBF=∠AFB,
∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠ABF=∠AFB,
∴AB=AF,
∵BO⊥AE,
∴∠AOB=∠EOB=90°,
∵BO=BO,
在△BOA和△BOE中,
 ,
,
∴△BOA≌△BOE(ASA),
∴AB=BE,
∴BE=AF,BE∥AF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形;
(2)解:菱形ABEF的周长为16,∠BEF=120°,
∴BE=AB=4,∠AEB=60°,
∴△ABE是等边三角形,则AE=AB=4.


练习册系列答案
相关题目