题目内容
【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
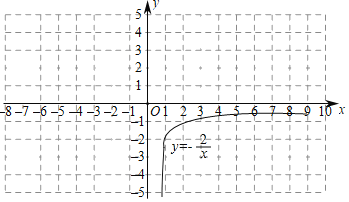
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2,﹣
﹣2,﹣![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.
【答案】(1)y=|![]() |-3;(2)1,-1;(3)当x>2时,y随x增大而增大;或当x<2时,y随x减小而减小;(4)2
|-3;(2)1,-1;(3)当x>2时,y随x增大而增大;或当x<2时,y随x减小而减小;(4)2![]() ﹣2≤x≤
﹣2≤x≤![]() +4
+4
【解析】
(1)由题意利用待定系数法构建方程组即可解决问题.
(2)由题意利用描点法即可解决问题.
(3)由题意观察图象,写出函数的性质即可.
(4)由题意求出点E,F的坐标即可解决问题.
解:(1)把x=0,y=﹣2;x=2,y=﹣3代入y=|kx﹣1|+b中,得
﹣2=|﹣1|+b,﹣3=|2k﹣1|﹣3
∴b=﹣3,∴k=![]() ,
,
∴y=|![]() |-3.
|-3.
(2)∵x=﹣6时,y=1,
x=6时,y=﹣1,
故答案为1,﹣1.
函数图象如图所示:
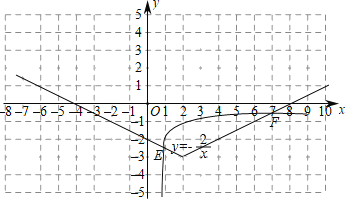
(3)当x>2时,y随x增大而增大;或当x<2时,y随x减小而减小.
(4)由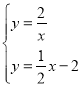 解得
解得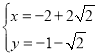 或
或 ,
,
∴E(﹣2+2![]() ,﹣1﹣
,﹣1﹣![]() ),
),
同法可得F(2![]() +4,﹣2+
+4,﹣2+![]() )
)
观察图象可知不等式|kx﹣1|+b≤![]() 的解集为:2
的解集为:2![]() ﹣2≤x≤
﹣2≤x≤![]() +4.
+4.