Question

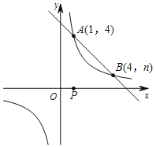
【题目】在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0）、B两点，与y轴交于点C （0，3），点P在该抛物线的对称轴上，且纵坐标为2．

（1）求抛物线的表达式以及点P的坐标；

（2）当三角形中一个内角α是另一个内角β的两倍时，我们称α为此三角形的“特征角”．

①当D在射线AP上，如果∠DAB为△ABD的特征角，求点D的坐标；

②点E为第一象限内抛物线上一点，点F在x轴上，CE⊥EF，如果∠CEF为△ECF的特征角，求点E的坐标．

Answer 1

【答案】（1）y＝﹣x2+2x+3；点P（1，2）；（2）①D（0，）或（3，4）；②点E（，）．

【解析】

（1）抛物线y＝﹣x2+bx+c与y轴交于点C （0，3），则c＝3，将点A的坐标代入抛物线表达式并解得：b＝2，即可求解；

（2）①当α＝60°，∠DBA＝β＝30°时，△ABD为直角三角形，即可求解；当∠ADB＝β时，则∠ABD＝90°，即可求解；

②∠CEF为△ECF的特征角，则△CEF为等腰直角三角形，则△CNE≌△EMF（AAS），即可求解．

解：

（1）∵抛物线y＝﹣x2+bx+c与y轴交于点C（0，3），则c＝3，

将点A的坐标代入抛物线表达式并解得：b＝2，

故抛物线的表达式为：y＝﹣x2+2x+3；

点P（1，2）；

（2）由点A、P的坐标知，∠PAB＝60，

直线AP的表达式为：y＝（x+1）…①，

当α＝60，∠DBA＝β＝30时，

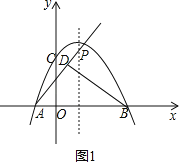
△ABD为直角三角形，由面积公式得：

yD×AB＝ADBD，即yD×4＝2×2，

解得：yD＝，

点D在AP上，故点D（0，）；

当∠ADB＝β时，则∠ABD＝90，

故点D（3，4）；

综上，点D的坐标为：（0，）或（3，4）；

（3）∠CEF为△ECF的特征角，则△CEF为等腰直角三角形，

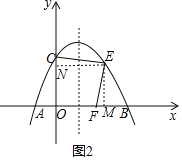
过点E分别作x轴、y轴的垂线交于点M、N，

则△CNE≌△EMF（AAS），

则EN＝EM，即x＝y，

x＝y＝﹣x2+2x+3，解得：x＝；

故点E（，）．