题目内容
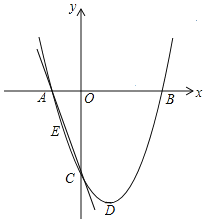
【题目】在平面直角坐标系中，二次函数y＝﹣x2+2x+3的图象交x轴于点A、B（点A在点B的左侧）．若把点B向上平移m（m＞0）个单位长度得点B1，若点B1向左平移n（n＞0）个单位长度，将与该二次函数图象上的点B2重合；若点B1向左平移（n+2）个单位长度，将与该二次函数图象上的点B3重合．则n的值为（ ）
A.1B.2C.3D.4
【答案】A
【解析】
根据题意写出B2，B3的坐标，再由对称轴方程列出n的方程，求得n即可得到答案．
解：（1）y＝0，则﹣x2+2x+3＝0，解得，x1＝3，x2＝﹣1，
∴B（3，0），
由题意得，B1（3，m），B2（3﹣n，m），B3（1﹣n，m），
函数图象的对称轴为直线x＝
＝1，
∵点B2，B3在二次函数图象上且纵坐标相同，
∴
＝1，
∴n＝1，
故选：A．
新非凡教辅冲刺100分系列答案
【题目】在函数学习中，我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．同时我们也学习了绝对值的意义
，结合上面经历的学习过程，现在来解决下面的问题：在函数y＝|kx﹣1|+b中，当x＝2时，y＝﹣3；x＝0时，y＝﹣2．
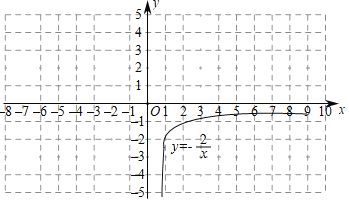
（1）求这个函数的表达式；
（2）用列表描点的方法画出该函数的图象；请你先把下面的表格补充完整，然后在下图所给的坐标系中画出该函数的图象；
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
（3）观察这个函数图象，并写出该函数的一条性质；
（4）已知函数y＝
（x＞0）的图象如图所示，与y＝|kx﹣1|+b的图象两交点的坐标分别是（2
+4，
－2），（2﹣2﹣1），结合你画的函数图象，直接写出|kx﹣1|+b≤的解集．
【题目】（本题满分10分）科幻小说《实验室的故事》中，有这样一个情节，科学家把一种珍奇的植物分别放在不同温度的环境中，经过一天后，测试出这种植物高度的增长情况（如下表）：
温度 | …… | －4 | －2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据，科学家推测出植物每天高度增长量
是温度
的函数，且这种函数是反比例函数、一次函数和二次函数中的一种．
（1）请你选择一种适当的函数，求出它的函数关系式，并简要说明不选择另外两种函数的理由；
（2）温度为多少时，这种植物每天高度的增长量最大？
（3）如果实验室温度保持不变，在10天内要使该植物高度增长量的总和超过250mm，那么实验室的温度应该在哪个范围内选择？请直接写出结果．
