题目内容
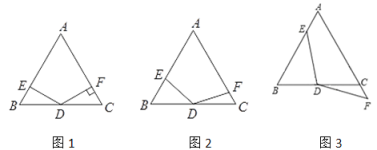
【题目】如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,M为AB边的中点,连结ME、MD、ED,设AB=10,∠DBE=30°,则△EDM的面积为____________

【答案】![]()
【解析】
根据条件可以判断△ABE和△ADB是直角三角形,且EM和DM分别时他们斜边上的中线,证明∠EMD=2∠DAC=60°,从而可得△DME是边长为5的等边三角形即可得出答案.
解:∵在△ABC中,AD⊥BC,垂足为点D,
BE⊥AC,垂足为点E,
∴△ABE,△ADB是直角三角形,
∴EM,DM分别是它们斜边上的中线,
EM=DM=![]() AB,
AB,
∵ME=![]() AB=MA,
AB=MA,
∴∠MAE=∠MEA.
∴∠BME=2∠MAE,
同理,MD=![]() AB=MA,
AB=MA,
∴∠MAD=∠MDA,
∴∠BMD=2∠MAD,
∴∠EMD=∠BME-∠BMD=2∠MAE-2∠M
所以△DEM是边长为5的等边三角形,所以
![]()
![]()
故选B.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
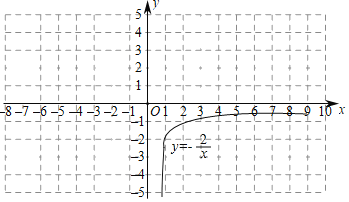
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2,﹣
﹣2,﹣![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.