题目内容
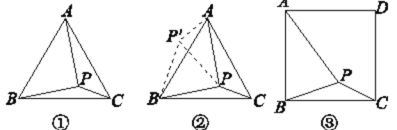
【题目】问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC的度数和等边三角形ABC的边长.
,PC=1,求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B= °,所以∠BPC=∠AP′B= °,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为 ,问题得到解决.
(1)根据李明同学的思路填空:∠AP′B= °,∠BPC=∠AP′B= °,等边三角形ABC的边长为 .
(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA=![]() ,PB=
,PB=![]() ,PC=1.求∠BPC的度数和正方形ABCD的边长.
,PC=1.求∠BPC的度数和正方形ABCD的边长.
【答案】(1)∠AP′B=150°,∠BPC=∠AP′B=150°,等边三角形ABC的边长为![]() ;(2)∠BPC=135°,正方形ABCD的边长为
;(2)∠BPC=135°,正方形ABCD的边长为![]() .
.
【解析】
根据旋转得出AP′=CP=1,BP′=BP=![]() ,∠PBC=∠P′BA,∠AP′B=∠BPC,求出∠ABP′+∠ABP=60°,得到等边△BPP′,推出PP′=
,∠PBC=∠P′BA,∠AP′B=∠BPC,求出∠ABP′+∠ABP=60°,得到等边△BPP′,推出PP′=![]() ,∠BP′P=60°,求出∠AP′P=90°即可求出∠BPC;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=
,∠BP′P=60°,求出∠AP′P=90°即可求出∠BPC;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=![]() ,P′M=
,P′M=![]() ,根据勾股定理即可求出答案;
,根据勾股定理即可求出答案;
(2)求出∠BEP=![]() (180°-90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
(180°-90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
(1)∵等边△ABC,
∴∠ABC=60°,
将△BPC绕点B逆时针旋转60°得出△ABP′,
∴AP′=CP=1,BP′=BP=![]() ,∠PBC=∠P′BA,∠AP′B=∠BPC,
,∠PBC=∠P′BA,∠AP′B=∠BPC,
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴PP′=![]() ,∠BP′P=60°,
,∠BP′P=60°,
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,
∴∠BPC=∠AP′B=90°+60°=150°,
过点B作BM⊥AP′,交AP′的延长线于点M,
∴∠MP′B=30°,BM=![]() ,
,
由勾股定理得:P′M=![]() ,
,
∴AM=1+![]() =
=![]() ,
,
由勾股定理得:AB=![]() ,
,
故答案为:150°,![]() .
.
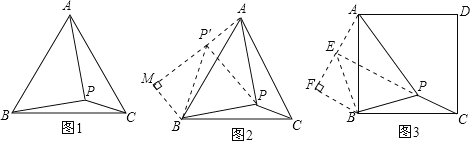
(2)将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=![]() ,∠BPC=∠AEB,∠ABE=∠PBC,
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴∠BEP=![]() (180°-90°)=45°,
(180°-90°)=45°,
由勾股定理得:EP=2,
∵AE=1,AP=![]() ,EP=2,
,EP=2,
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°,
过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.
答:∠BPC的度数是135°,正方形ABCD的边长是![]() .
.

 阅读快车系列答案
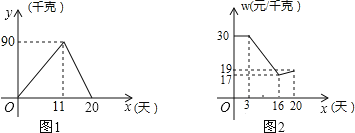
阅读快车系列答案【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
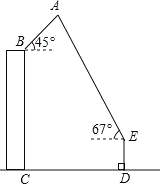
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
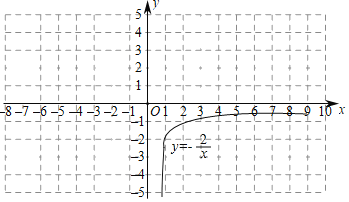
【题目】在函数学习中,我们经历了“确定函数表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时我们也学习了绝对值的意义![]() ,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
,结合上面经历的学习过程,现在来解决下面的问题:在函数y=|kx﹣1|+b中,当x=2时,y=﹣3;x=0时,y=﹣2.
(1)求这个函数的表达式;
(2)用列表描点的方法画出该函数的图象;请你先把下面的表格补充完整,然后在下图所给的坐标系中画出该函数的图象;
x | … | ﹣6 | ﹣4 | ﹣2 | 0 | 2 | 4 | 6 | … |
y | … |
| 0 | ﹣1 | ﹣2 | ﹣3 | ﹣2 |
| … |
(3)观察这个函数图象,并写出该函数的一条性质;
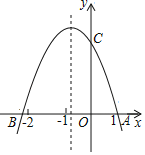
(4)已知函数y=![]() (x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2
(x>0)的图象如图所示,与y=|kx﹣1|+b的图象两交点的坐标分别是(2![]() +4,
+4,![]() -2),(2
-2),(2![]() ﹣2,﹣
﹣2,﹣![]() ﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤
﹣1),结合你画的函数图象,直接写出|kx﹣1|+b≤![]() 的解集.
的解集.