题目内容
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( ) 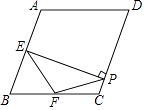
A.55°
B.50°
C.45°
D.35°
【答案】A
【解析】解:延长PF交AB的延长线于点G.如图所示: 在△BGF与△CPF中, 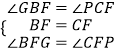 ,
,
∴△BGF≌△CPF(ASA),
∴GF=PF,
∴F为PG中点.
又∵由题可知,∠BEP=90°,
∴EF= ![]() PG,
PG,
∵PF= ![]() PG,
PG,
∴EF=PF,
∴∠FEP=∠EPF,
∵∠BEP=∠EPC=90°,
∴∠BEP﹣∠FEP=∠EPC﹣∠EPF,即∠BEF=∠FPC,
∵四边形ABCD为菱形,
∴AB=BC,∠ABC=180°﹣∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE= ![]() (180°﹣70°)=55°,
(180°﹣70°)=55°,
∴∠FPC=55°;
故选:A.
【考点精析】根据题目的已知条件,利用菱形的性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
相关题目
【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |
(1)根据上述统计图可得此次采访的人数为人,m= , n=;
(2)根据以上信息补全条形统计图; 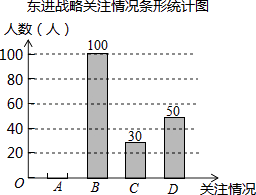
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.