题目内容
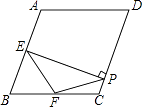
【题目】如图,顶点为(1,4)的抛物线y=ax2+bx+c与直线y= ![]() x+n交于点A(2,2),直线y=
x+n交于点A(2,2),直线y= ![]() x+n与y轴交于点B与x轴交于点C
x+n与y轴交于点B与x轴交于点C
(1)求n的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在x轴上,求点P的坐标
(3)点D为x轴上方抛物线上的一点,点E为轴上一点,以A、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标.
【答案】
(1)
解:A(2,2)代入 ![]() 得n=1
得n=1
设抛物线的解析式y=a(x﹣1)2+4代入点A(2,2),可得a=﹣2
所以抛物线的解析式y=2(x﹣1)2+4=﹣2x2+4x+2
(2)
解:如图1.
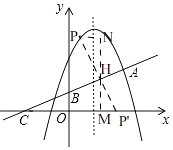
设PP'与AC的交点为H,
作HM⊥x轴于M,作PN⊥HM与N
设 ![]() ,
,
∵点P'是点P关于AC的对称点,
∴PH=P'H,
易得,△HNP≌△HMP',
∴MH=NH,
∴NM=2NH,
∴﹣2x2+4x+2=m+2,
∴m=﹣2x2+4x①
∵直线AC的解析式为y= ![]() x+1,
x+1,
∴B(0,1),C(﹣2,0),
∴OB=1,OC=2,
∵OB∥HM,
∴△COB∽△CMH,
∴ ![]() ,
,
∴CM=2MH,
易证,△HMP'∽△CMH,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴MH=2P'M=2PN
∴ ![]() ,
,
∴4x=3m﹣2②
联立①②解得x=1或 ![]() ,
,
∴点P的坐标(1,4)或 ![]()
(3)
解:设点E坐标为A(t,0),以AB为边或对角线进行分类讨论:
①如图4,当AB是平行四边行的边时,AB∥DE,AB=DE
由于点B(0,1)先向右平移2个单位,再向上平移1个单位得到A(2,2),
∴点D的坐标可以表示为D(t+2,1)
将D(t+2,1)代入y=2(x﹣1)2+4,得﹣2(t+1)2+4=1
解得 ![]() ,
,
此时 ![]() 或
或 ![]() ,
,
②当AB是平行四边形的对角线时,
设AB的中点 ![]() ,点E(t,0),
,点E(t,0),
关于 ![]() 的对称点D的坐标可以表示为(2﹣t,3)
的对称点D的坐标可以表示为(2﹣t,3)
将D(2﹣t,3)代入y=﹣2(x﹣1)2+4,得﹣2(1﹣t)2+4=3
解得 ![]() ,
,
∴ ![]() 或
或 ![]() .
.

【解析】(1)利用待定系数法先求出n的值,进而求出抛物线解析式(2)先利用对称性判断出MN=2NH,进而建立方程化简得到m=﹣2x2+4x①,再判断出△COB∽△CMH和△HMP'∽△CMH,判断出MH=2PN,进而建立方程化简得出4x=3m﹣2②联立方程组求解即可;(3)分AB为平行四边形的对角线和边即可得出点E的坐标.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 阅读快车系列答案
阅读快车系列答案【题目】问题情境
已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ ![]() )(x>0)
)(x>0)
探索研究
(1)我们可以借鉴学习函数的经验,先探索函数y=x+ ![]() (x>0)的图象性质.
(x>0)的图象性质.
①列表:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … |
| m |
| 2 |
|
|
| … |
表中m=;
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;
(2)解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+ ![]() (x>0)的最小值.
(x>0)的最小值.
y=x+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() ﹣2
﹣2 ![]()
![]() +2
+2 ![]()
![]() =
= ![]() +2
+2
∵ ![]() ≥0,∴y≥2
≥0,∴y≥2
∴当 ![]() ﹣
﹣ ![]() =0,即x=1时,y最小值=2
=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.
【题目】2015年榕城区从中随机调查了5所初中九年级学生的数学考试成绩,学生的考试成绩情况如表(数学考试满分120分)
分数段 | 频数 | 频率 |
72分以下 | 368 | 0.2 |
72﹣﹣﹣﹣80分 | 460 | 0.25 |
81﹣﹣﹣﹣95分 | ||
96﹣﹣﹣﹣108分 | 184 | 0.2 |
109﹣﹣﹣﹣119分 | ||
120分 | 54 |
(1)这5所初中九年级学生的总人数有多少人?
(2)统计时,老师漏填了表中空白处的数据,请你帮老师填上;
(3)从这5所初中九年级学生中随机抽取一人,恰好是108分以上(不包括108分)的概率是多少?