题目内容
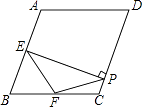
【题目】如图,已知△ABC内接于⊙O,AD为边上的高,将△ADC沿直线AC翻折得到△AEC,延长EA交⊙O于点P,连接FC,交AB于N. 
(1)求证:∠BAC=∠ABC+∠ACF;
(2)求证:EF=DB;
(3)若AD=5,CD=10,CB∥AF,求点F到AB的距离.
【答案】
(1)证明:如图1中,∵△ADC沿直线AC翻折得到△AEC,
∴∠BAC=∠EAC=∠ACF+∠F,
∵∠F=∠ABC,
∴∠BAC=∠ABC+∠ACF.

(2)在△CEF和△CDB中,

∴△CEF≌△CDB,
∴EF=BD.
(3)由四边形AECD,可证得∠BAF=∠ECD=2∠ACD,
取AC中点H作HG⊥AC,交CE于点G,则GC=GA,
∴∠EGA=2∠GCA=∠ECD,
设GC=GA=x,则EG=10﹣x,
在Rt△AEG中,52+(10﹣x)2=x2,
∴x= ![]() ,
,
∴tan∠EGA= ![]() ,
,
∵BC∥AF,
tanB=tan∠BAF= ![]() ,
,
设AF=a,BD=EF=5+a
tanB= ![]() =
= ![]() =
= ![]() ,
,
∴a= ![]() ,
,
在Rt△AMF中,∵tan∠FAM= ![]() =
= ![]() ,AF=
,AF= ![]() ,
,
∴FM=2.

【解析】(1)由△ADC沿直线AC翻折得到△AEC,可得∠BAC=∠EAC=∠ACF+∠F,又∠F=∠ABC,即可推出∠BAC=∠ABC+∠ACF;(2)只要证明△CEF≌△CDB,即可推出EF=BD;(3)首先证明tan∠EGA=tanB=tan∠BAF= ![]() ,设AF=a,BD=EF=5+a,构建tanB=
,设AF=a,BD=EF=5+a,构建tanB= ![]() =
= ![]() =
= ![]() ,推出a=
,推出a= ![]() ,在Rt△AMF中,构建tan∠FAM=
,在Rt△AMF中,构建tan∠FAM= ![]() =
= ![]() ,即可推出AF=
,即可推出AF= ![]() ,即可解决问题;
,即可解决问题;

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案【题目】问题情境
已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ ![]() )(x>0)
)(x>0)
探索研究
(1)我们可以借鉴学习函数的经验,先探索函数y=x+ ![]() (x>0)的图象性质.
(x>0)的图象性质.
①列表:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … |
| m |
| 2 |
|
|
| … |
表中m=;
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;
(2)解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+ ![]() (x>0)的最小值.
(x>0)的最小值.
y=x+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() ﹣2
﹣2 ![]()
![]() +2
+2 ![]()
![]() =
= ![]() +2
+2
∵ ![]() ≥0,∴y≥2
≥0,∴y≥2
∴当 ![]() ﹣
﹣ ![]() =0,即x=1时,y最小值=2
=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.