题目内容
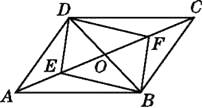
【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,直线l交CD边于点E,连接BE.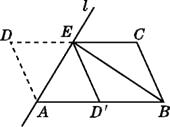
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
【答案】
(1)证明:由折叠的性质可得∠DAE=∠D'AE,∠DEA=∠D'EA,DA=D'A.
∵DE∥AD',∴∠DEA=∠EAD',
∴∠DAE=∠EAD'=∠DEA.
∴DE=DA=AD'.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC
∴CE∥D'B,CE=D'B,
∴四边形BCED'是平行四边形
(2)证明:∵BE平分∠ABC,∴∠CBE=∠EBA.
∵AD∥BC,∴∠DAB+∠CBA=180°.
∵∠DAE=∠BAE,∴∠EAB+∠EBA=90°.
∴∠AEB=90°.∴AB2=AE2+BE2
【解析】(1)根据折叠的性质得出∠DAE=∠D'AE,∠DEA=∠D'EA,DA=D'A.,再根据平行四边形的性质及平行线的性质证明DE=AD',就可证明四边形ABCD是平行四边形,再证明CE∥D'B,CE=D'B,,就可证明四边形BCED'是平行四边形。
(2)根据角平分线的定义及平行线的性质证明△ABE是直角三角形,再利用勾股定理即可证得结论。

练习册系列答案
相关题目