题目内容
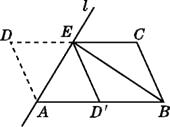
【题目】如图1,已知:矩形ABCD中,AC、BD是对角线,分别延长AD至E,延长CD至F,使得DE=AD,DF=CD.
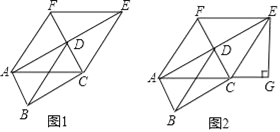
(1)求证:四边形ACEF为菱形.
(2)如图2,过E作EG⊥AC的延长线于G,若AG=8,cos∠ECG=![]() ,则AD= (直接填空)
,则AD= (直接填空)
【答案】(1)证明见解析;(2)2![]() .
.
【解析】试题分析:(1)先证明四边形ACEF是平行四边形,再由矩形的性质证出AE⊥CF,即可得出四边形ACEF是菱形;
(2)由菱形的性质得出AC=CE,AD=ED,与三角函数得出CG=![]() CE=
CE=![]() AC,得出CG=3,CE=AC=5,由勾股定理求出EG=
AC,得出CG=3,CE=AC=5,由勾股定理求出EG=![]() =4,在Rt△AEG中,由勾股定理求出AE=
=4,在Rt△AEG中,由勾股定理求出AE=![]() =4
=4![]() ,即可得出AD的长.
,即可得出AD的长.
试题解析:(1)∵DE=AD,DF=CD.∴四边形ACEF是平行四边形,
∵四边形ABCD是矩形,∴∠ADC=90°,
∴AE⊥CF,∴四边形ACEF是菱形;
(2)∵四边形ACEF是菱形,∴AC=CE,AD=ED,
∵EG⊥AC,cos∠ECG=![]() =
=![]() ,∴CG=
,∴CG=![]() CE=
CE=![]() AC,
AC,
∵AG=AC+CG=8,∴CG=3,CE=AC=5,∴EG=![]() =4,
=4,
在Rt△AEG中,AE=![]() =
=![]() =4
=4![]() ,∴AD=
,∴AD=![]() AE=2
AE=2![]() ;
;
故答案为:2![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目